题目内容
15．不等式$\frac{3-x}{x+1}$＜0的解集是（-∞，-1）∪（3，+∞）．分析 将分式不等式等价转化后，由一元二次不等式的解法求出解集即可．
解答 解：不等式$\frac{3-x}{x+1}＜0$等价于（x+1）（3-x）＜0，
即（x+1）（x-3）＞0，解得x＜-1或x＞3，
所以不等式的解集是（-∞，-1）∪（3，+∞），
故答案为：（-∞，-1）∪（3，+∞）．
点评 本题考查简单的分式不等式的解法，以及一元二次不等式的解法，考查转化思想．
练习册系列答案
相关题目
6．一个物体的运动方程为s=t2-t+2（其中s的单位是米，t的单位是秒），那么物体在t=4秒的瞬时速度是（ ）
| A． | 6米/秒 | B． | 7米/秒 | C． | 8米/秒 | D． | 9米/秒 |
3．已知sin（30°+α）=$\frac{3}{5}$，60°＜α＜150°，则cosα的值是（ ）
| A． | $\frac{3\sqrt{3}-4}{10}$ | B． | $\frac{4}{5}$ | C． | $\frac{3+4\sqrt{3}}{10}$ | D． | $\frac{3-4\sqrt{3}}{10}$ |
10．双曲线$\frac{{x}^{2}}{4}$-y2=1的离心率为（ ）
| A． | $\frac{1}{2}$ | B． | $\sqrt{5}$ | C． | $\frac{\sqrt{3}}{2}$ | D． | $\frac{\sqrt{5}}{2}$ |
20．若经过A（a，-1），B（2，3）的直线的斜率为2，则a等于（ ）
| A． | 0 | B． | -1 | C． | 1 | D． | -2 |
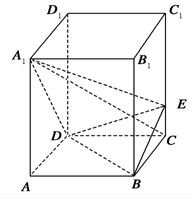如图，正四棱柱ABCD-A1B1C1D1中，AA1=2AB=4，点E在CC1上且C1E=3EC．