题目内容
13.柜子里有3双不同的鞋,随机地取2只,下列叙述错误的是( )| A. | 取出的鞋不成对的概率是$\frac{4}{5}$ | |
| B. | 取出的鞋都是左脚的概率是$\frac{1}{5}$ | |
| C. | 取出的鞋都是同一只脚的概率是$\frac{2}{5}$ | |
| D. | 取出的鞋一只是左脚的,一只是右脚的,但它们不成对的概率是$\frac{12}{25}$ |
分析 利用等可能事件概率计算公式分别求解,能求出结果.
解答 解:∵柜子里有3双不同的鞋,随机地取2只,
∴基本事件总数n=${C}_{6}^{2}$=15,
在A中,取出的鞋是成对的取法有3种,
∴取出的鞋不成对的概率是:1-$\frac{3}{15}$=$\frac{4}{5}$,故A 正确;
在B中,取出的鞋都是左脚的取法有${C}_{3}^{2}$=3种,
∴取出的鞋都是左脚的概率为:$\frac{3}{15}=\frac{1}{5}$,故B正确;
在C中,取出的鞋都是同一只脚的取法有:${C}_{3}^{2}+{C}_{3}^{2}$=6,
∴取出的鞋都是同一只脚的概率是p=$\frac{6}{15}$=$\frac{2}{5}$;
在D中,取出的鞋一只是左脚的,一只是右脚的,
由题意,可以先选出左脚的一只有${C}_{3}^{1}$=3种选法,
然后从剩下两双的右脚中选出一只有${C}_{2}^{1}$=2种选法,
所以一共6种取法,
∴取出的鞋一只是左脚的,一只是右脚的,但它们不成对的概率是$\frac{6}{15}=\frac{2}{5}$,故D错误.
故选:D.
点评 本题考查概率的求法,是基础题,解题时要认真审题,注意等可能事件概率计算公式的合理运用.

练习册系列答案
相关题目
4.直线x=-$\frac{p}{2}$和圆x2+y2+6x+8=0相切,则实数p=( )
| A. | p=4 | B. | p=8 | C. | p=4或p=8 | D. | p=2或p=4 |
18.如图,位于A处前方有两个观察站B,D,且△ABD为边长等于3km的正三角形,当发现目标出现于C处时,测得∠BDC=45°,∠CBD=75°,则AC=( )
| A. | 15-6$\sqrt{3}$km | B. | 15+6$\sqrt{3}$km | C. | $\sqrt{15+6\sqrt{3}}$km | D. | $\sqrt{15-6\sqrt{3}}$km |
2.圆柱的体积为π,底面半径为1,则该圆柱的侧面积为( )
| A. | $\frac{π}{2}$ | B. | π | C. | $\frac{3π}{2}$ | D. | 2π |
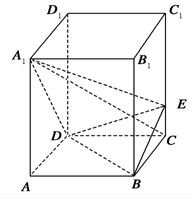 如图,正四棱柱ABCD-A1B1C1D1中,AA1=2AB=4,点E在CC1上且C1E=3EC.
如图,正四棱柱ABCD-A1B1C1D1中,AA1=2AB=4,点E在CC1上且C1E=3EC.