题目内容
15.已知$\frac{tanα}{tanα-1}$=-1,(1)求$\frac{sinα-2cosα}{sinα+cosα}$的值;
(2)求sin2α+sinαcosα的值.
分析 (1)由题意求得tanα的值,再利用同角三角函数的基本关系,求得要求式子的值.
(2)利用同角三角函数的基本关系化简要求的式子,再把tanα的值代入,可得要求式子的值.
解答 解:∵已知$\frac{tanα}{tanα-1}$=-1,∴tanα=$\frac{1}{2}$,
∴(1)$\frac{sinα-2cosα}{sinα+cosα}$=$\frac{tanα-2}{tanα+1}$=-1;
(2)sin2α+sinαcosα=$\frac{{sin}^{2}α+sinαcosα}{{sin}^{2}α{+cos}^{2}α}$=$\frac{{tan}^{2}α+tanα}{{tan}^{2}α+1}$=$\frac{3}{5}$.
点评 本题主要考查同角三角函数的基本关系的应用,属于基础题.

练习册系列答案
相关题目
10.双曲线$\frac{{x}^{2}}{4}$-y2=1的离心率为( )
| A. | $\frac{1}{2}$ | B. | $\sqrt{5}$ | C. | $\frac{\sqrt{3}}{2}$ | D. | $\frac{\sqrt{5}}{2}$ |
4.直线x=-$\frac{p}{2}$和圆x2+y2+6x+8=0相切,则实数p=( )
| A. | p=4 | B. | p=8 | C. | p=4或p=8 | D. | p=2或p=4 |
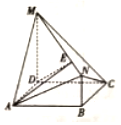 如图,四边形ABCD是矩形,MD⊥平面ABCD,NB∥MD,且AD=2,NB=1,CD=MD=3.
如图,四边形ABCD是矩形,MD⊥平面ABCD,NB∥MD,且AD=2,NB=1,CD=MD=3.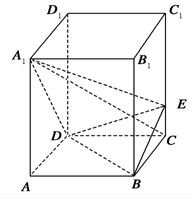 如图,正四棱柱ABCD-A1B1C1D1中,AA1=2AB=4,点E在CC1上且C1E=3EC.
如图,正四棱柱ABCD-A1B1C1D1中,AA1=2AB=4,点E在CC1上且C1E=3EC.