题目内容
12.已知抛物线4y=x2,则它的焦点坐标是( )| A. | (0,2) | B. | (1,0) | C. | (2,0) | D. | (0,1) |
分析 根据题意,由抛物线的方程分析可得其焦点在y轴正半轴上,且p=2,由焦点坐标公式计算可得答案.
解答 解:根据题意,抛物线的方程为4y=x2,即x2=4y,
其焦点在y轴正半轴上,且p=2,
则其焦点坐标为(0,1);
故选:D.
点评 本题考查抛物线的几何性质,注意要先由标准方程分析焦点位置.

练习册系列答案
相关题目
6.一个物体的运动方程为s=t2-t+2(其中s的单位是米,t的单位是秒),那么物体在t=4秒的瞬时速度是( )
| A. | 6米/秒 | B. | 7米/秒 | C. | 8米/秒 | D. | 9米/秒 |
4.直线x=-$\frac{p}{2}$和圆x2+y2+6x+8=0相切,则实数p=( )
| A. | p=4 | B. | p=8 | C. | p=4或p=8 | D. | p=2或p=4 |
2.圆柱的体积为π,底面半径为1,则该圆柱的侧面积为( )
| A. | $\frac{π}{2}$ | B. | π | C. | $\frac{3π}{2}$ | D. | 2π |
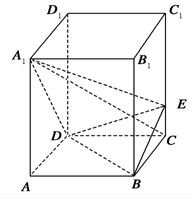 如图,正四棱柱ABCD-A1B1C1D1中,AA1=2AB=4,点E在CC1上且C1E=3EC.
如图,正四棱柱ABCD-A1B1C1D1中,AA1=2AB=4,点E在CC1上且C1E=3EC.