题目内容
在极坐标系中，直线ρcosθ-ρsinθ-3=0与圆ρ=2cosθ的位置关系是（ ）
| A、相交但不过圆心 | B、相交且过圆心 |
| C、相离 | D、相切 |
考点：简单曲线的极坐标方程
专题：计算题,坐标系和参数方程
分析：化直线ρcosθ-ρsinθ-3=0可化为x-y-3=0，圆ρ=2cosθ可化为x2+y2=2x，从而判断直线与圆的位置关系．
解答：
解：直线ρcosθ-ρsinθ-3=0可化为x-y-3=0，
圆ρ=2cosθ可化为x2+y2=2x，
即（x-1）2+y2=1，
又∵
=
＞1，
则线ρcosθ-ρsinθ-3=0与圆ρ=2cosθ相离．
故选D．
圆ρ=2cosθ可化为x2+y2=2x，
即（x-1）2+y2=1，
又∵
| |1-0-3| | ||
|
| 2 |
则线ρcosθ-ρsinθ-3=0与圆ρ=2cosθ相离．
故选D．
点评：本题考查了一般方程与参数方程的互化，属于基础题．
练习册系列答案
相关题目
经过双曲线x2-y2=8的右焦点且斜率为2的直线被双曲线截得的线段的长是（ ）
A、
| ||||
B、7
| ||||
C、2
| ||||
D、
|
若函数f（x）=|ax|-x-a（a＞0）有两个零点，则a的取值范围是（ ）
| A、（1，+∞） | B、（0，1） |
| C、（0，+∞） | D、∅ |
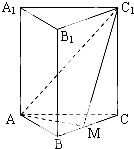如图，正三棱柱ABC-A1B1C1的底面边长为1，点M在BC上，△AMC1是以M为直角顶点的等腰直角三角形．双曲线
-y2=1的离心率的值是（ ）
| x2 |
| 4 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|