题目内容
已知函数f（x）=|x+1|+|x-2|；
（1）解不等式f（x）≥5；
（2）若对任意实数x，不等式|x+1|+|x-2|＞ax恒成立，求实数a的取值范围．
（1）解不等式f（x）≥5；
（2）若对任意实数x，不等式|x+1|+|x-2|＞ax恒成立，求实数a的取值范围．
考点：绝对值不等式的解法,函数的图象,分段函数的应用
专题：不等式的解法及应用
分析：（1）由条件根据绝对值的意义，数轴上的-2和3对应点到-1、2对应点的距离之和正好等于5，从而求得不等式f（x）≥5的解集．
（2）由题意可得f（x）的图象恒在直线y=ax的上方．再根据f（x）=
，画出图形，数形结合求得a的范围．
（2）由题意可得f（x）的图象恒在直线y=ax的上方．再根据f（x）=
|
解答：
解：（1）函数f（x）=|x+1|+|x-2|表示数轴上的x对应点到-1、2对应点的距离之和，
而数轴上的-2和3对应点到-1、2对应点的距离之和正好等于5，故不等式f（x）≥5的解集为{x|x≤-2，或 x≥3}．
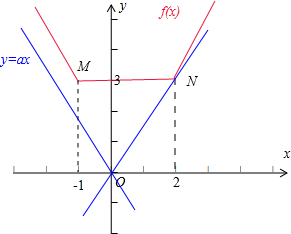
（2）由于不等式|x+1|+|x-2|＞ax恒成立，即f（x）＞ax恒成立，即f（x）的图象恒在直线y=ax的上方．
再根据f（x）=
，画出图形，如图：
故直线y=ax的斜率a满足-2≤a＜
，即a的范围为[-2，
）．
解：（1）函数f（x）=|x+1|+|x-2|表示数轴上的x对应点到-1、2对应点的距离之和，而数轴上的-2和3对应点到-1、2对应点的距离之和正好等于5，故不等式f（x）≥5的解集为{x|x≤-2，或 x≥3}．
（2）由于不等式|x+1|+|x-2|＞ax恒成立，即f（x）＞ax恒成立，即f（x）的图象恒在直线y=ax的上方．
再根据f（x）=
|
故直线y=ax的斜率a满足-2≤a＜
| 3 |
| 2 |
| 3 |
| 2 |
点评：本题主要考查绝对值的意义，带由绝对值的函数，函数的恒成立问题，体现了转化、数形结合的数学思想，属于基础题．
练习册系列答案
相关题目
已知定点M（0，1），N（1，-1），Q（1，0），动点P满足2