题目内容
设函数f(x)=
cos2ωx+sinωxcosωx+a,(ω>0,a∈R),且f(x)的图象在y轴右侧的第一个最高点的横坐标为
.
(Ⅰ)求ω的值及对称轴方程:
(Ⅱ)如果f(x)在区间[-
,
]上的最小值为
,求a的值.
| 3 |
| π |
| 6 |
(Ⅰ)求ω的值及对称轴方程:
(Ⅱ)如果f(x)在区间[-
| π |
| 3 |
| 5π |
| 6 |
| 3 |
考点:三角函数中的恒等变换应用,函数y=Asin(ωx+φ)的图象变换
专题:三角函数的求值,三角函数的图像与性质
分析:(Ⅰ)先对三角函数式进行恒等变换,变换成正弦型函数然后根据题中的条件,进一步确定ω的值及对称轴方程.
(Ⅱ)根据第一步求得的结果,依据在区间[-
,
]上的最小值为
,进一步求得a的值.
(Ⅱ)根据第一步求得的结果,依据在区间[-
| π |
| 3 |
| 5π |
| 6 |
| 3 |
解答:
解:(Ⅰ)函数f(x)=
cos2ωx+sinωxcosωx+a=
cos2ωx+
sin2ωx+
+a=sin(2ωx+
)+
+a
∵f(x)的图象在y轴右侧的第一个最高点的横坐标为
∴2ω
+
=
解得ω=
∴函数f(x)=sin(x+
)+
+a的对称轴方程
令x+
=kπ+
(k∈Z)
解得 x=kπ+
(k∈Z)
故函数f(x)的对称轴方程为:x=kπ+
(k∈Z)
(Ⅱ)由(1)得f(x)=sin(x+
)+
+a
∵x∈[-
,
]
∴x+
∈[0,
]
∴-
≤sin(x+
)≤1
从而函数f(x)在[-
,
]取得的最小值为-
+
+a
∴由题设f(x)在区间[-
,
]上的最小值为
则
+
+a=
即 a=
故答案为:
(1)ω=
函数f(x)的对称轴方程为:x=kπ+
(k∈Z)
(2)a=
| 3 |
| ||
| 2 |
| 1 |
| 2 |
| ||
| 2 |
| π |
| 3 |
| ||
| 2 |
∵f(x)的图象在y轴右侧的第一个最高点的横坐标为
| π |
| 6 |
∴2ω
| π |
| 6 |
| π |
| 3 |
| π |
| 2 |
| 1 |
| 2 |
∴函数f(x)=sin(x+
| π |
| 3 |
| ||
| 2 |
令x+
| π |
| 3 |
| π |
| 2 |
解得 x=kπ+
| π |
| 6 |
故函数f(x)的对称轴方程为:x=kπ+
| π |
| 6 |
(Ⅱ)由(1)得f(x)=sin(x+
| π |
| 3 |
| ||
| 2 |
∵x∈[-
| π |
| 3 |
| 5π |
| 6 |
∴x+
| π |
| 3 |
| 7π |
| 6 |
∴-
| 1 |
| 2 |
| π |
| 3 |
从而函数f(x)在[-
| π |
| 3 |
| 5π |
| 6 |
| 1 |
| 2 |
| ||
| 2 |
∴由题设f(x)在区间[-
| π |
| 3 |
| 5π |
| 6 |
| 3 |
则
| 1 |
| 2 |
| ||
| 2 |
| 3 |
即 a=
| ||
| 2 |
故答案为:
(1)ω=
| 1 |
| 2 |
| π |
| 6 |
(2)a=
| ||
| 2 |
点评:本题的重点是考察三角函数式的恒等变换、对称轴方程、以及在某一定义域下的值域,是高招的重点题型.

练习册系列答案
相关题目
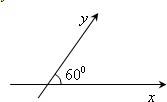 如图,在平面斜坐标系xoy中,∠xoy=60°,平面上任一点P在斜坐标系
如图,在平面斜坐标系xoy中,∠xoy=60°,平面上任一点P在斜坐标系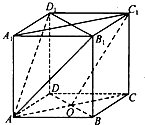 如图,在正方体ABCD-A1B1C1D1中,O是底面ABCD对角线的交点.
如图,在正方体ABCD-A1B1C1D1中,O是底面ABCD对角线的交点.