题目内容
已知四棱锥S-ABCD的所有棱长都相等,E是SB的中点,求AE、SD所成的角的正弦值.
考点:异面直线及其所成的角
专题:空间角
分析:通过建立空间直角坐标系,利用向量的夹角公式即可得出异面直线所成的夹角.
解答:
解:如图所示,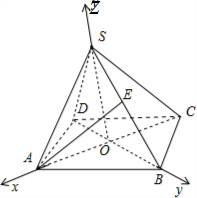
∵四棱锥S-ABCD的所有棱长都相等,设|AB|=
.
∴A(1,0,0),B(0,1,0),S(0,0,1),
D(0,-1,0),E(0,
,
).
=(-1,
,
),
=(0,-1,-1).
∴cos<
,
>=
=
=-
.
∴设AE、SD所成的角为θ.
则sinθ=
=
.
∴AE、SD所成的角的正弦值为
.

∵四棱锥S-ABCD的所有棱长都相等,设|AB|=
| 2 |
∴A(1,0,0),B(0,1,0),S(0,0,1),
D(0,-1,0),E(0,
| 1 |
| 2 |
| 1 |
| 2 |
| AE |
| 1 |
| 2 |
| 1 |
| 2 |
| SD |
∴cos<
| AE |
| SD |
| ||||
|
|
| -1 | ||||||
|
| ||
| 3 |
∴设AE、SD所成的角为θ.
则sinθ=
1-(-
|
| ||
| 3 |
∴AE、SD所成的角的正弦值为
| ||
| 3 |
点评:本题考查了利用向量的夹角公式求出异面直线所成的夹角的方法,属于基础题.

练习册系列答案
相关题目
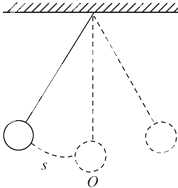 如图,单摆从某点开始来回摆动,离开平衡位置O的距离s cm和时间t s的函数关系式为s=6sin(2πt+
如图,单摆从某点开始来回摆动,离开平衡位置O的距离s cm和时间t s的函数关系式为s=6sin(2πt+| π |
| 6 |
| A、2π s |
| B、π s |
| C、0.5 s |
| D、1 s |