题目内容
6.根据条件回答下列问题:(1)求函数y=lg(tanx)的定义域;
(2)求函数$y=\frac{3sinx+1}{sinx-2}$的值域.
分析 (1)利用tanx>0,可得x∈(kπ,kπ+$\frac{π}{2}$),(k∈Z),可得函数y=lg(tanx)的定义域;
(2)分离常数可得y=3+$\frac{7}{sinx-2}$,由-1≤sinx≤1和不等式的性质可得.
解答 解:(1)由tanx>0,可得x∈(kπ,kπ+$\frac{π}{2}$),(k∈Z)
∴函数y=lg(tanx)的定义域为(kπ,kπ+$\frac{π}{2}$),(k∈Z);
(2)分离常数可得y=3+$\frac{7}{sinx-2}$,
∵-1≤sinx≤1,∴-3≤sinx-2≤-1,∵-7≤$\frac{7}{sinx-2}$≤-$\frac{7}{3}$,
∴-4≤3+$\frac{7}{sinx-2}$≤$\frac{2}{3}$,即函数的值域为[-4,$\frac{2}{3}$].
点评 本题考查函数的定义域,考查三角函数的最值,分离常数并利用不等式的性质是解决问题的关键,属基础题.

练习册系列答案
相关题目
14.三棱锥的棱长均为4$\sqrt{6}$,顶点在同一球面上,则该球的表面积为( )
| A. | 36π | B. | 72π | C. | 144π | D. | 288π |
1.下列四个函数中在(0,+∞)上为增函数的是( )
| A. | f(x)=3-x | B. | f(x)=(x-1)2 | C. | f(x)=$\frac{1}{x}$ | D. | f(x)=x2+2x |
18.如图,PA垂直于矩形ABCD所在的平面,则图中与平面PCD垂直的平面是( )
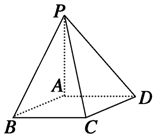

| A. | 平面ABCD | B. | 平面PBC | C. | 平面PAD | D. | 平面PBC |
15.已知(1,1)是直线l被椭圆$\frac{{x}^{2}}{36}$+$\frac{{y}^{2}}{9}$=1所截得的线段的中点,则l的斜率是( )
| A. | $-\frac{1}{2}$ | B. | $\frac{1}{2}$ | C. | $-\frac{1}{4}$ | D. | $\frac{1}{4}$ |
16.直线x+$\sqrt{3}$y+k=0的倾斜角是( )
| A. | $\frac{5}{6}$π | B. | $\frac{2π}{3}$ | C. | $\frac{π}{3}$ | D. | $\frac{π}{6}$ |