题目内容
已知函数f(x)=ax2+
+5(其中常数a,b∈R)满足f(2)+f(-2)=26.
(Ⅰ)若f(-1)=-2000,求f(1);
(Ⅱ)若函数φ(x)=xf(x)+2x+2-x(x∈(0,1))的值域为(0,
),求b的值;
(Ⅲ)在(Ⅱ)的条件下
①证明f(x)恰有一个零点;
②给出一个增函数g(x)使得当x∈N+时,g(x)∈N+,且
=rg(1)+rg(2)+rg(3)+…+rg(n)+…成立.
(已知等式
=1+q+q2+…+qn-1+…对任意实数q∈(-1,1)恒成立)
| b |
| x |
(Ⅰ)若f(-1)=-2000,求f(1);
(Ⅱ)若函数φ(x)=xf(x)+2x+2-x(x∈(0,1))的值域为(0,
| 15 |
| 2 |
(Ⅲ)在(Ⅱ)的条件下
①证明f(x)恰有一个零点;
②给出一个增函数g(x)使得当x∈N+时,g(x)∈N+,且
| 2 |
| 5 |
(已知等式
| 1 |
| 1-q |
考点:函数与方程的综合运用
专题:函数的性质及应用
分析:(Ⅰ)根据条件建立方程求出a的值,根据f(-1)=-2000,即可求f(1);
(Ⅱ)根据函数的单调性的定义判断函数的单调性,结合值域关系即可得到结论;
(Ⅲ)构造g(x)=x,令r=
即可.
(Ⅱ)根据函数的单调性的定义判断函数的单调性,结合值域关系即可得到结论;
(Ⅲ)构造g(x)=x,令r=
| 2 |
| 7 |
解答:
解:(Ⅰ)由f(x)=ax2+
+5,得f(2)+f(-2)=8a+10,
因为f(2)+f(-2)=26,所以8a+10=26,即a=2.
所以f(1)+f(-1)=a+b+5+a-b+5=2a+10=14,
又f(-1)=-2000,故f(1)=2014;
(Ⅱ)由(Ⅰ)得a=2,所以φ(x)=xf(x)+2x+2-x
=2x3+5x+b+2x+2-x,
令h(x)=2x+2-x,设0≤x1<x2≤1,
则h(x1)-h(x2)=2x1+2-x1-2x2-2-x2
=
,
因为0≤x1<x2≤1,所以2x1-2x2<0,2x1+x2-1>0,
所以h(x1)-h(x2)<0,即h(x1)<h(x2),
所以h(x)在(0,1)上为增函数,
又因为函数y=2x3与函数y=5x+b在(0,1)上均为增函数,
所以φ(x)在(0,1)上为增函数,
所以φ(x)在(0,1)上的值域为(b+2,b+
),
又因为φ(x)在(0,1)上的值域为(0,
),
所以
,
解得b=-2,
所以b的值是-2;
(Ⅲ)①由(Ⅰ)、(Ⅱ)得a=2,b=-2,
所以f(x)=2x2-
+5.
当x<0时,f(x)>0恒成立,
所以f(x)在(-∞,0)上没有零点;
当x>0时,由于函数y=2x2+5与函数y=-
均在(0,+∞)上单调递增,
所以f(x)=2x2-
+5在(0,+∞)上单调递增.
又f(1)=5>0,f(
)=
-3<0,
即f(1)•f(
)<0,
所以f(x)恰有一个零点;
②令g(x)=x,则
函数g(x)=x是增函数,当x∈N+时,g(x)∈N+,
此时
+1=1+r1+r2+r3+…+rn+…
=
,解得r=
,
故当给出的增函数为g(x)=x,r=
时满足题意.
| b |
| x |
因为f(2)+f(-2)=26,所以8a+10=26,即a=2.
所以f(1)+f(-1)=a+b+5+a-b+5=2a+10=14,
又f(-1)=-2000,故f(1)=2014;
(Ⅱ)由(Ⅰ)得a=2,所以φ(x)=xf(x)+2x+2-x
=2x3+5x+b+2x+2-x,
令h(x)=2x+2-x,设0≤x1<x2≤1,
则h(x1)-h(x2)=2x1+2-x1-2x2-2-x2
=
| (2x1-2x2)(2x1+x2-1) |
| 2x1+x2 |
因为0≤x1<x2≤1,所以2x1-2x2<0,2x1+x2-1>0,
所以h(x1)-h(x2)<0,即h(x1)<h(x2),
所以h(x)在(0,1)上为增函数,
又因为函数y=2x3与函数y=5x+b在(0,1)上均为增函数,
所以φ(x)在(0,1)上为增函数,
所以φ(x)在(0,1)上的值域为(b+2,b+
| 19 |
| 2 |
又因为φ(x)在(0,1)上的值域为(0,
| 15 |
| 2 |
所以
|
解得b=-2,
所以b的值是-2;
(Ⅲ)①由(Ⅰ)、(Ⅱ)得a=2,b=-2,
所以f(x)=2x2-
| 2 |
| x |
当x<0时,f(x)>0恒成立,
所以f(x)在(-∞,0)上没有零点;
当x>0时,由于函数y=2x2+5与函数y=-
| 2 |
| x |
所以f(x)=2x2-
| 2 |
| x |
又f(1)=5>0,f(
| 1 |
| 4 |
| 1 |
| 8 |
即f(1)•f(
| 1 |
| 4 |
所以f(x)恰有一个零点;
②令g(x)=x,则
函数g(x)=x是增函数,当x∈N+时,g(x)∈N+,
此时
| 2 |
| 5 |
=
| 1 |
| 1-r |
| 2 |
| 7 |
故当给出的增函数为g(x)=x,r=
| 2 |
| 7 |
点评:本题考查函数性质的综合应用,求出函数的解析式是解决本题的关键.要求熟练掌握函数性质的综合应用.

练习册系列答案
 优质课堂快乐成长系列答案
优质课堂快乐成长系列答案
相关题目
已知复数z=a+(a-2)i(a∈R,i为虚数单位)为实数,则
(
+x)dx的值为( )
| ∫ | a 0 |
| 4-x2 |
| A、2+π | ||
B、2+
| ||
| C、4+2π | ||
| D、4+4π |
曲线y=xn(x∈N)在点P(
,(
)n)处的切线的斜率为20,则n为( )
| 2 |
| 2 |
| A、7 | B、6 | C、5 | D、4 |
已知:α,β是不同的平面,l,m,n是不同的直线,则下列说法正确的是( )
A、
| |||||||
B、
| |||||||
C、
| |||||||
D、
|
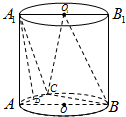 如图,平面ABB1A1为圆柱OO1的轴截面,点C为底面圆周上异于A,B的任意一点.
如图,平面ABB1A1为圆柱OO1的轴截面,点C为底面圆周上异于A,B的任意一点.