题目内容
5.如果直线3ax+y-1=0与直线(1-2a)x+ay+1=0平行.那么a等于( )| A. | -1 | B. | $\frac{1}{3}$ | C. | 3 | D. | -1或$\frac{1}{3}$ |
分析 由直线的平行关系可得a的方程,解方程排除直线重合即可.
解答 解:∵直线3ax+y-1=0与直线(1-2a)x+ay+1=0平行,
∴3a•a=1•(1-2a),解得a=-1或a=$\frac{1}{3}$,
经检验当a=-1时,两直线重合,应舍去,
故选:B.
点评 本题考查直线的一般式方程和平行关系,属基础题.

练习册系列答案
相关题目
16.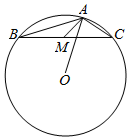 已知△ABC外接圆的圆心为O,$AB=2\sqrt{3}$,$AC=2\sqrt{2}$,A为钝角,M是BC边的中点,则$\overrightarrow{AM}•\overrightarrow{AO}$=( )
已知△ABC外接圆的圆心为O,$AB=2\sqrt{3}$,$AC=2\sqrt{2}$,A为钝角,M是BC边的中点,则$\overrightarrow{AM}•\overrightarrow{AO}$=( )
 已知△ABC外接圆的圆心为O,$AB=2\sqrt{3}$,$AC=2\sqrt{2}$,A为钝角,M是BC边的中点,则$\overrightarrow{AM}•\overrightarrow{AO}$=( )
已知△ABC外接圆的圆心为O,$AB=2\sqrt{3}$,$AC=2\sqrt{2}$,A为钝角,M是BC边的中点,则$\overrightarrow{AM}•\overrightarrow{AO}$=( )| A. | 3 | B. | 4 | C. | 5 | D. | 6 |
14.一圆锥的侧面积是其底面积的2倍,若圆锥的高为$\sqrt{3}$,则其表面积为( )
| A. | $\frac{3\sqrt{3}π}{2}$ | B. | 6π | C. | 3π | D. | 3$\sqrt{3}$π |
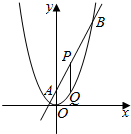 已知抛物线C:x2=2py(p>0)的焦点为F,直线l:y=2x+2交抛物线C于A,B两点,P是线段AB的中点,过P作x轴的垂直交抛物线C于点Q.
已知抛物线C:x2=2py(p>0)的焦点为F,直线l:y=2x+2交抛物线C于A,B两点,P是线段AB的中点,过P作x轴的垂直交抛物线C于点Q.