题目内容
3.设a=21.2,b=log38,c=0.83.1,则( )| A. | b<a<c | B. | c<a<b | C. | c<b<a | D. | a<c<b |
分析 利用指数函数和对数函数的性质求解.
解答 解:∵a=21.2>21=2,
1=log33<b=log38<log39=2,
c=0.83.1<0.81=0.8,
∴c<b<a.
故选:C.
点评 本题考查三个数大小的比较,是基础题,解题时要认真审题,注意对数函数、指数函数的性质的合理运用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
11.设$\frac{π}{2}$<α<π,若sin(α+$\frac{π}{6}$)=$\frac{1}{3}$,则cos($\frac{2π}{3}$+α)=( )
| A. | -$\frac{2\sqrt{2}}{3}$ | B. | $\frac{2\sqrt{2}}{3}$ | C. | -$\frac{1}{3}$ | D. | $\frac{1}{3}$ |
12.在四面体ABCD中,E、G分别是CD、BE的中点,若$\overrightarrow{AG}$=x$\overrightarrow{AB}$+y$\overrightarrow{AD}$+z$\overrightarrow{AC}$,则x+y+z=( )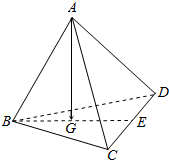

| A. | $\frac{1}{3}$ | B. | $\frac{1}{2}$ | C. | 1 | D. | 2 |
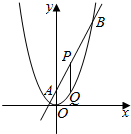 已知抛物线C:x2=2py(p>0)的焦点为F,直线l:y=2x+2交抛物线C于A,B两点,P是线段AB的中点,过P作x轴的垂直交抛物线C于点Q.
已知抛物线C:x2=2py(p>0)的焦点为F,直线l:y=2x+2交抛物线C于A,B两点,P是线段AB的中点,过P作x轴的垂直交抛物线C于点Q.