题目内容
4.已知p:方程方程 $\frac{{x}^{2}}{m-1}$+$\frac{{y}^{2}}{2-m}$=1表示焦点在y轴上的椭圆;q:实数m满足m2-(2a+1)m+a2+a<0且¬q是¬p的充分不必要条件,求实数a的取值范围.分析 由p可得:2-m>m-1>0,解得m范围.由q:实数m满足m2-(2a+1)m+a2+a<0化为:(m-a)[m-(a+1)]<0,解得m范围.
又¬q是¬p的充分不必要条件,可得p⇒q.
解答 解:由p可得:2-m>m-1>0,解得$1<m<\frac{3}{2}$.
由q:实数m满足m2-(2a+1)m+a2+a<0化为:(m-a)[m-(a+1)]<0,解得a<m<a+1.
又¬q是¬p的充分不必要条件,∴p⇒q.
则$\left\{\begin{array}{l}{a≤1}\\{\frac{3}{2}≤a+1}\end{array}\right.$,解得$\frac{1}{2}≤a≤1$.经过检验a=$\frac{1}{2}$或1时均适合题意.
故a的取值范围是$\frac{1}{2}≤a≤1$.
点评 本题考查了不等式的解法、简易逻辑的判定方法,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
12.在四面体ABCD中,E、G分别是CD、BE的中点,若$\overrightarrow{AG}$=x$\overrightarrow{AB}$+y$\overrightarrow{AD}$+z$\overrightarrow{AC}$,则x+y+z=( )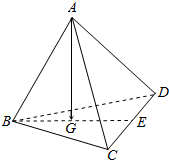

| A. | $\frac{1}{3}$ | B. | $\frac{1}{2}$ | C. | 1 | D. | 2 |
19.已知a,b为非零实数,且a<b,则下列结论一定成立的是( )
| A. | a2<b2 | B. | a3<b3 | C. | $\frac{1}{a}$>$\frac{1}{b}$ | D. | ac2<bc2 |
9.已知四面体ABCD,$\overrightarrow{DA}$=$\overrightarrow{a}$,$\overrightarrow{DB}$=$\overrightarrow{b}$,$\overrightarrow{DC}$=$\overrightarrow{c}$,点M在棱DA上,$\overrightarrow{DM}$=2$\overrightarrow{MA}$,N为BC中点,则$\overrightarrow{MN}$=( )
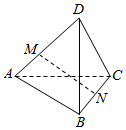

| A. | -$\frac{2}{3}$$\overrightarrow{a}$-$\frac{1}{2}$$\overrightarrow{b}$-$\frac{1}{2}$$\overrightarrow{c}$ | B. | -$\frac{2}{3}$$\overrightarrow{a}$+$\frac{1}{2}$$\overrightarrow{b}$+$\frac{1}{2}$$\overrightarrow{c}$ | C. | $\frac{2}{3}$$\overrightarrow{a}$+$\frac{1}{2}$$\overrightarrow{b}$+$\frac{1}{2}$$\overrightarrow{c}$ | D. | $\frac{2}{3}$$\overrightarrow{a}$-$\frac{1}{2}$$\overrightarrow{b}$-$\frac{1}{2}$$\overrightarrow{c}$ |
16.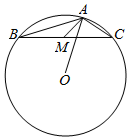 已知△ABC外接圆的圆心为O,$AB=2\sqrt{3}$,$AC=2\sqrt{2}$,A为钝角,M是BC边的中点,则$\overrightarrow{AM}•\overrightarrow{AO}$=( )
已知△ABC外接圆的圆心为O,$AB=2\sqrt{3}$,$AC=2\sqrt{2}$,A为钝角,M是BC边的中点,则$\overrightarrow{AM}•\overrightarrow{AO}$=( )
 已知△ABC外接圆的圆心为O,$AB=2\sqrt{3}$,$AC=2\sqrt{2}$,A为钝角,M是BC边的中点,则$\overrightarrow{AM}•\overrightarrow{AO}$=( )
已知△ABC外接圆的圆心为O,$AB=2\sqrt{3}$,$AC=2\sqrt{2}$,A为钝角,M是BC边的中点,则$\overrightarrow{AM}•\overrightarrow{AO}$=( )| A. | 3 | B. | 4 | C. | 5 | D. | 6 |
14.一圆锥的侧面积是其底面积的2倍,若圆锥的高为$\sqrt{3}$,则其表面积为( )
| A. | $\frac{3\sqrt{3}π}{2}$ | B. | 6π | C. | 3π | D. | 3$\sqrt{3}$π |
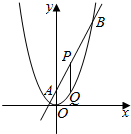 已知抛物线C:x2=2py(p>0)的焦点为F,直线l:y=2x+2交抛物线C于A,B两点,P是线段AB的中点,过P作x轴的垂直交抛物线C于点Q.
已知抛物线C:x2=2py(p>0)的焦点为F,直线l:y=2x+2交抛物线C于A,B两点,P是线段AB的中点,过P作x轴的垂直交抛物线C于点Q.