题目内容
8.在△ABC中,角A、B、C的对边分别为a、b、c,面积为S,已知$2a{cos^2}\frac{C}{2}+2c{cos^2}\frac{A}{2}=\frac{5}{2}b$(Ⅰ)求证:2(a+c)=3b;
(Ⅱ)若$cosB=\frac{1}{4}$,$S=\sqrt{15}$,求b.
分析 (Ⅰ)由已知及降幂公式可得$a(1+cosC)+c(1+cosA)=\frac{5}{2}b$,由acosC+ccosA=b,可得$a+c=\frac{3}{2}b$,即可得解.
(Ⅱ)利用同角三角函数基本关系式可求$sinB=\frac{{\sqrt{15}}}{4}$,利用三角形面积公式可求ac=8,利用余弦定理可得b2=(a+c)2-2ac(1+cosB),代入(Ⅰ)的结论2(a+c)=3b,即可解得b的值.
解答 (本小题满分12分)
解:(Ⅰ)由条件:$a(1+cosC)+c(1+cosA)=\frac{5}{2}b$,
由于:acosC+ccosA=b,所以:$a+c=\frac{3}{2}b$,
即:2(a+c)=3b….(5分)
(Ⅱ)∵$cosB=\frac{1}{4}$,∴$sinB=\frac{{\sqrt{15}}}{4}$,….(6分)
∵$S=\frac{1}{2}acsinB=\frac{1}{8}\sqrt{15}ac=\sqrt{15}$,∴ac=8….(8分)
又∵b2=a2+c2-2accosB=(a+c)2-2ac(1+cosB),
由2(a+c)=3b,
∴$\frac{{5{b^2}}}{4}=16(1+\frac{1}{4})$,
∴b=4….(12分)
点评 本题主要考查了降幂公式,同角三角函数基本关系式,三角形面积公式,余弦定理在解三角形中的综合应用,考查了计算能力和转化思想,属于中档题.

练习册系列答案
相关题目
19.已知a,b为非零实数,且a<b,则下列结论一定成立的是( )
| A. | a2<b2 | B. | a3<b3 | C. | $\frac{1}{a}$>$\frac{1}{b}$ | D. | ac2<bc2 |
16.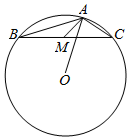 已知△ABC外接圆的圆心为O,$AB=2\sqrt{3}$,$AC=2\sqrt{2}$,A为钝角,M是BC边的中点,则$\overrightarrow{AM}•\overrightarrow{AO}$=( )
已知△ABC外接圆的圆心为O,$AB=2\sqrt{3}$,$AC=2\sqrt{2}$,A为钝角,M是BC边的中点,则$\overrightarrow{AM}•\overrightarrow{AO}$=( )
 已知△ABC外接圆的圆心为O,$AB=2\sqrt{3}$,$AC=2\sqrt{2}$,A为钝角,M是BC边的中点,则$\overrightarrow{AM}•\overrightarrow{AO}$=( )
已知△ABC外接圆的圆心为O,$AB=2\sqrt{3}$,$AC=2\sqrt{2}$,A为钝角,M是BC边的中点,则$\overrightarrow{AM}•\overrightarrow{AO}$=( )| A. | 3 | B. | 4 | C. | 5 | D. | 6 |
18.设全集U={0,1,2,3,4},∁UA={1,2},B={1,3},则A∪B等于( )
| A. | {2} | B. | {1,2,3} | C. | {0,1,3,4} | D. | {0,1,2,3,4} |