题目内容
已知函数f(x)=ax2-
x-
(a>0),若在任意长度为2的闭区间上总存在两点x1、x2,使得|f(x1)-f(x2)|≥
成立,则a的最小值为 .
| 1 |
| 2 |
| 3 |
| 4 |
| 1 |
| 4 |
考点:二次函数的性质
专题:函数的性质及应用
分析:要使函数f(x)在任意长度为2的闭区间上总存在两点x1,x2,使|f(x1)-f(x2)|≥
成立,只需要|f(
-1)-f(
)|≥
恒成立,从而可求实数a的最小值
| 1 |
| 4 |
| 1 |
| 4a |
| 1 |
| 4a |
| 1 |
| 4 |
解答:
解:要使函数f(x)=ax2-
x-
(a>0)在任意长度为2的闭区间上总存在两点x1,x2,使|f(x1)-f(x2)|≥
成立,
只需要|f(
-1)-f(
)|≥
恒成立
∵f(x)=ax2-
x-
=a(x-
)2-
-
,
∴|f(
-1)-f(
)|=|a|≥
∵a>0
∴a≥
∴实数a的最小值为
故答案为:
| 1 |
| 2 |
| 3 |
| 4 |
| 1 |
| 4 |
只需要|f(
| 1 |
| 4a |
| 1 |
| 4a |
| 1 |
| 4 |
∵f(x)=ax2-
| 1 |
| 2 |
| 3 |
| 4 |
| 1 |
| 4a |
| 1 |
| 16a |
| 3 |
| 4 |
∴|f(
| 1 |
| 4a |
| 1 |
| 4a |
| 1 |
| 4 |
∵a>0
∴a≥
| 1 |
| 4 |
∴实数a的最小值为
| 1 |
| 4 |
故答案为:
| 1 |
| 4 |
点评:本题以新定义为素材,考查对新定义的理解,考查学生分析解决问题的能力,解题的关键是将问题转化为恒成立.

练习册系列答案
相关题目
设
<a<π,sinα=
,则
的值为( )
| π |
| 2 |
| 4 |
| 5 |
| sin2α+sin2α |
| cos2α+cos2α |
| A、8 | B、10 | C、-4 | D、-20 |
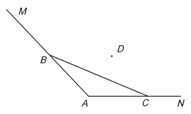 在一个六角形体育馆的一角MAN内,用长为a的围栏设置一个运动器材储存区域(如图所示),已知∠A=120°,B是墙角线AM上的一点,C是墙角线AN上的一点.
在一个六角形体育馆的一角MAN内,用长为a的围栏设置一个运动器材储存区域(如图所示),已知∠A=120°,B是墙角线AM上的一点,C是墙角线AN上的一点.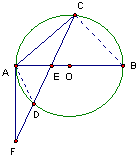 如图,已知AB是⊙O的直径,弦CD与AB交于点E,过点A作圆的切线与CD的延长线交于点F,如果DE=
如图,已知AB是⊙O的直径,弦CD与AB交于点E,过点A作圆的切线与CD的延长线交于点F,如果DE=