题目内容
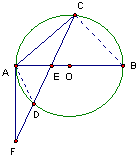 如图,已知AB是⊙O的直径,弦CD与AB交于点E,过点A作圆的切线与CD的延长线交于点F,如果DE=
如图,已知AB是⊙O的直径,弦CD与AB交于点E,过点A作圆的切线与CD的延长线交于点F,如果DE=| 3 |
| 4 |
| 5 |
考点:与圆有关的比例线段
专题:
分析:连接AD,BC,设CE=4x,AE=y,则DF=DE=3x,EF=6x.利用圆的切线的性质,可得△EAF为直角三角形,由勾股定理得:EF2=AE2+AF2,建立关于x,y的关系式,再设BE=z,由相交弦定理得到y,z的关系式,从而能求出x,y,z的值,问题的解.
解答:
 解:连接AD,BC.
解:连接AD,BC.
设CE=4x,AE=y,则DF=DE=3x,EF=6x
∵AB为⊙O的直径,AF为⊙O的切线,
∴∠EAF=90°,∠ACD=∠DAF.
又∵D为Rt△AEF的斜边EF的中点,
∴DA=DE=DF,
∴∠DAF=∠AFD,
∴∠ACD=∠AFD,
∴AF=AC=8
.
在Rt△AEF中,由勾股定理得EF2=AE2+AF2,即36x2=y2+320.
设BE=z,由相交弦定理得CE•DE=AE•BE,即yz=4x•3x=12x2,
∴y2+320=3yz①
又∵AD=DE,
∴∠DAE=∠AED.
又∵∠DAE=∠BCE,∠AED=∠BEC,
∴∠BCE=∠BEC,从而BC=BE=z.
在Rt△ACB中,由勾股定理得AB2=AC2+BC2,即(y+z)2=320+z2,
∴y2+2yz=320.②
联立①②,解得y=8,z=16.
∴AB=AE+BE=24.
故答案为:24.
 解:连接AD,BC.
解:连接AD,BC.设CE=4x,AE=y,则DF=DE=3x,EF=6x
∵AB为⊙O的直径,AF为⊙O的切线,
∴∠EAF=90°,∠ACD=∠DAF.
又∵D为Rt△AEF的斜边EF的中点,
∴DA=DE=DF,
∴∠DAF=∠AFD,
∴∠ACD=∠AFD,
∴AF=AC=8
| 5 |
在Rt△AEF中,由勾股定理得EF2=AE2+AF2,即36x2=y2+320.
设BE=z,由相交弦定理得CE•DE=AE•BE,即yz=4x•3x=12x2,
∴y2+320=3yz①
又∵AD=DE,
∴∠DAE=∠AED.
又∵∠DAE=∠BCE,∠AED=∠BEC,
∴∠BCE=∠BEC,从而BC=BE=z.
在Rt△ACB中,由勾股定理得AB2=AC2+BC2,即(y+z)2=320+z2,
∴y2+2yz=320.②
联立①②,解得y=8,z=16.
∴AB=AE+BE=24.
故答案为:24.
点评:本题考查了圆的切线的性质;勾股定理;相交弦定理,以及用方程思想解决几何问题,综合性很强,有一定的难度.

练习册系列答案
相关题目
设集合M={x|x≤-1或x≥1},N={y|y=lgx2,1≤x≤10},则(∁RM)∩N=( )
| A、[-1,0) |
| B、[-1,1] |
| C、[0,1] |
| D、[0,1) |
 如图所示是根据输入的x计算y值的程序框图,若x依次取数列{
如图所示是根据输入的x计算y值的程序框图,若x依次取数列{| n2+4 |
| n |
| A、4 | B、8 | C、16 | D、32 |
若l,m为空间两条不同的直线,α,β为空间两个不同的平面,则l丄α的一个充分条件是( )
| A、l∥β且α丄β |
| B、l?β且α丄β |
| C、l丄β且α∥β |
| D、l丄m且m∥α |
