题目内容
19.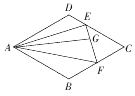 如图,在平行四边形ABCD中,$DE=\frac{1}{2}EC$,F为BC的中点,G为EF上的一点,且$\overrightarrow{AG}=m\overrightarrow{AB}+\frac{2}{3}\overrightarrow{AD}$,则实数m的值为( )
如图,在平行四边形ABCD中,$DE=\frac{1}{2}EC$,F为BC的中点,G为EF上的一点,且$\overrightarrow{AG}=m\overrightarrow{AB}+\frac{2}{3}\overrightarrow{AD}$,则实数m的值为( )| A. | $\frac{7}{9}$ | B. | $-\frac{2}{9}$ | C. | $-\frac{1}{9}$ | D. | $\frac{5}{9}$ |
分析 由题意可知$\overrightarrow{AE}$=$\overrightarrow{AD}$+$\overrightarrow{DE}$=$\frac{1}{3}$$\overrightarrow{AB}$+$\overrightarrow{AD}$,$\overrightarrow{AF}$=$\overrightarrow{AB}$+$\overrightarrow{BF}$=$\overrightarrow{AB}$+$\frac{1}{2}$$\overrightarrow{AD}$,根据向量的共线定理$\overrightarrow{AG}$=λ$\overrightarrow{AE}$+(1-λ)$\overrightarrow{AF}$,列方程即可求得m和λ的值.
解答 解:由$\overrightarrow{AE}$=$\overrightarrow{AD}$+$\overrightarrow{DE}$=$\frac{1}{3}$$\overrightarrow{AB}$+$\overrightarrow{AD}$,
$\overrightarrow{AF}$=$\overrightarrow{AB}$+$\overrightarrow{BF}$=$\overrightarrow{AB}$+$\frac{1}{2}$$\overrightarrow{AD}$,
由E,F,G三点共线,
则$\overrightarrow{AG}$=λ$\overrightarrow{AE}$+(1-λ)$\overrightarrow{AF}$,
由$\overrightarrow{AG}=m\overrightarrow{AB}+\frac{2}{3}\overrightarrow{AD}$,
∴$\frac{1+λ}{2}$=$\frac{2}{3}$,m=$\frac{3-2λ}{3}$,
解得:λ=$\frac{1}{3}$,m=$\frac{7}{9}$,
∴实数m的值为$\frac{7}{9}$,
故选A.
点评 本题考查向量的加法,向量的共线定理,考查计算能力,数形结合思想,属于中档题.

| A. | 3 | B. | 6 | C. | 18 | D. | 9 |
| A. | 向左平移$\frac{1}{5}$个单位长度 | B. | 向右平移$\frac{π}{5}$个单位长度 | ||
| C. | 向右平移$\frac{1}{5}$个单位长度 | D. | 向左平移$\frac{π}{5}$个单位长度 |

 +
+
 的值的一个程序框图,则判断框内应填入的条件是 .
的值的一个程序框图,则判断框内应填入的条件是 .