题目内容
14.关于函数$f(x)=4sin(2x+\frac{π}{3}),x∈$R有下列命题:①函数 y=f(x)的最小正周期是π.
②函数y=f(x)的初相是$2x+\frac{π}{3}$.
③函数y=f(x)的振幅是4.
其中正确的是①③.
分析 根据函数y=Asin(ωx+φ)的图象和性质,得出结论.
解答 解:对于函数f(x)=4sin(2x+$\frac{π}{3}$),它的最小正周期是$\frac{2π}{2}$=π,故①正确;
它的初相为$\frac{π}{3}$,故②错误;
它的振幅为4,故③正确,
故答案为:①③.
点评 本题主要考查函数y=Asin(ωx+φ)的图象和性质,属于基础题.

练习册系列答案
 芝麻开花课程新体验系列答案
芝麻开花课程新体验系列答案 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案
相关题目
19.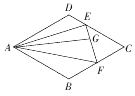 如图,在平行四边形ABCD中,$DE=\frac{1}{2}EC$,F为BC的中点,G为EF上的一点,且$\overrightarrow{AG}=m\overrightarrow{AB}+\frac{2}{3}\overrightarrow{AD}$,则实数m的值为( )
如图,在平行四边形ABCD中,$DE=\frac{1}{2}EC$,F为BC的中点,G为EF上的一点,且$\overrightarrow{AG}=m\overrightarrow{AB}+\frac{2}{3}\overrightarrow{AD}$,则实数m的值为( )
 如图,在平行四边形ABCD中,$DE=\frac{1}{2}EC$,F为BC的中点,G为EF上的一点,且$\overrightarrow{AG}=m\overrightarrow{AB}+\frac{2}{3}\overrightarrow{AD}$,则实数m的值为( )
如图,在平行四边形ABCD中,$DE=\frac{1}{2}EC$,F为BC的中点,G为EF上的一点,且$\overrightarrow{AG}=m\overrightarrow{AB}+\frac{2}{3}\overrightarrow{AD}$,则实数m的值为( )| A. | $\frac{7}{9}$ | B. | $-\frac{2}{9}$ | C. | $-\frac{1}{9}$ | D. | $\frac{5}{9}$ |
6.若函数f(x)=x3+x2+(a+6)x+a有极大值和极小值,则( )
| A. | $a>-\frac{17}{3}$ | B. | $a≥-\frac{17}{3}$ | C. | $a<-\frac{17}{3}$ | D. | $a≤-\frac{17}{3}$ |
2.设a>b,c>d则下列不等式中一定成立的是( )
| A. | a+c>b+d | B. | ac>bd | C. | a-c>b-d | D. | a+d>b+c |