题目内容
7．为了得到函数$y=cos（x+\frac{π}{5}）$，x∈R的图象，只需把余弦曲线y=cosx上的所有的点（ ）| A． | 向左平移$\frac{1}{5}$个单位长度 | B． | 向右平移$\frac{π}{5}$个单位长度 | ||
| C． | 向右平移$\frac{1}{5}$个单位长度 | D． | 向左平移$\frac{π}{5}$个单位长度 |
分析 根据函数y=Asin（ωx+φ）的图象变换规律，可得结论．
解答 解：把余弦曲线y=cosx上的所有的点向左平移$\frac{π}{5}$个单位长度，
可得函数y=cos（x+$\frac{π}{5}$）的图象，
故选：D．
点评 本题主要考查函数y=Asin（ωx+φ）的图象变换规律，属于基础题．
练习册系列答案
相关题目
19．
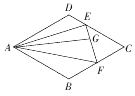如图，在平行四边形ABCD中，$DE=\frac{1}{2}EC$，F为BC的中点，G为EF上的一点，且$\overrightarrow{AG}=m\overrightarrow{AB}+\frac{2}{3}\overrightarrow{AD}$，则实数m的值为（ ）
如图，在平行四边形ABCD中，$DE=\frac{1}{2}EC$，F为BC的中点，G为EF上的一点，且$\overrightarrow{AG}=m\overrightarrow{AB}+\frac{2}{3}\overrightarrow{AD}$，则实数m的值为（ ）| A． | $\frac{7}{9}$ | B． | $-\frac{2}{9}$ | C． | $-\frac{1}{9}$ | D． | $\frac{5}{9}$ |
15．在用反证法证明“在△ABC中，若∠C是直角，则∠A和∠B都是锐角”的过程中，应该假设（ ）
| A． | ∠A和∠B都不是锐角 | B． | ∠A和∠B不都是锐角 | ||
| C． | ∠A和∠B都是钝角 | D． | ∠A和∠B都是直角 |