题目内容
8.设函数f(x)=x3+ax2+bx+5,曲线y=f(x)在点(1,f(1))处的切线方程为y=3x+1.(1)求f(x)的表达式;
(2)求y=f(x)在[-3,1]上的最大值.
分析 (1)由已知切线的方程可得切点坐标和切线的斜率,求出f(x)的导数,可得切线的斜率,解关于a,b的方程组,即可得到所求f(x)的解析式;
(2)求出f(x)的导数,并分解因式,求出在区间(-3,1)的单调区间和极值,求得f(-3)和f(1),比较即可得到所求最大值.
解答 解:(1)∵y=f(x)在点(1,f(1))处的切线方程为y=3x+1,
∴f(1)=3×1+1=4且切线的斜率为f'(1)=3.
又∵f'(x)=3x2+2ax+b,
∴$\left\{\begin{array}{l}f(1)=1+a+b+5=4\\ f'(1)=3+2a+b=3\end{array}\right.$,
∴$\left\{\begin{array}{l}a=2\\ b=-4\end{array}\right.$,
∴f(x)=x3+2x2-4x+5.
(2)由(1)知,f(x)=x3+2x2-4x+5,
∴f'(x)=3x2+4x-4=(x+2)(3x-2).
令f'(x)=0,则x=-2或$x=\frac{2}{3}$,
列表:
| x | -3 | (-3,-2) | -2 | $(-2,\frac{2}{3})$ | $\frac{2}{3}$ | $(\frac{2}{3},1)$ | 1 |
| f'(x) | + | 0 | - | 0 | + | ||
| f(x) | 8 | 递增 | 极大 | 递减 | 极小 | 递增 | 4 |
∴f(x)max=f(-2)=13.
点评 本题考查导数的运用:求切线的斜率和单调区间、极值和最值,考查运算能力,正确求导和运用直线方程是解题的关键,属于中档题.

练习册系列答案
 期末集结号系列答案
期末集结号系列答案
相关题目
19.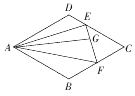 如图,在平行四边形ABCD中,$DE=\frac{1}{2}EC$,F为BC的中点,G为EF上的一点,且$\overrightarrow{AG}=m\overrightarrow{AB}+\frac{2}{3}\overrightarrow{AD}$,则实数m的值为( )
如图,在平行四边形ABCD中,$DE=\frac{1}{2}EC$,F为BC的中点,G为EF上的一点,且$\overrightarrow{AG}=m\overrightarrow{AB}+\frac{2}{3}\overrightarrow{AD}$,则实数m的值为( )
 如图,在平行四边形ABCD中,$DE=\frac{1}{2}EC$,F为BC的中点,G为EF上的一点,且$\overrightarrow{AG}=m\overrightarrow{AB}+\frac{2}{3}\overrightarrow{AD}$,则实数m的值为( )
如图,在平行四边形ABCD中,$DE=\frac{1}{2}EC$,F为BC的中点,G为EF上的一点,且$\overrightarrow{AG}=m\overrightarrow{AB}+\frac{2}{3}\overrightarrow{AD}$,则实数m的值为( )| A. | $\frac{7}{9}$ | B. | $-\frac{2}{9}$ | C. | $-\frac{1}{9}$ | D. | $\frac{5}{9}$ |
19.已知抛物线y2=2px(p>0)的焦点为F,P、Q是抛物线上的两点,若△FPQ是边长为2的正三角形,则p的值是( )
| A. | $2±\sqrt{3}$ | B. | $2+\sqrt{3}$ | C. | $\sqrt{3}±1$ | D. | $\sqrt{3}-1$ |
20.现要完成下列3项抽样调查:
①从10盒酸奶中抽取3盒进行食品卫生检查.
②科技报告厅有32排,每排有40个座位,有一次报告会恰好坐满了听众,报告会结束后,为了听取意见,
需要请32名听众进行座谈.
③高新中学共有160名教职工,其中一般教师120名,行政人员16名,后勤人员24名,为了了解教职工对学校在
校务公开方面的意见,拟抽取一个容量为20的样本.
较为合理的抽样方法是( )
①从10盒酸奶中抽取3盒进行食品卫生检查.
②科技报告厅有32排,每排有40个座位,有一次报告会恰好坐满了听众,报告会结束后,为了听取意见,
需要请32名听众进行座谈.
③高新中学共有160名教职工,其中一般教师120名,行政人员16名,后勤人员24名,为了了解教职工对学校在
校务公开方面的意见,拟抽取一个容量为20的样本.
较为合理的抽样方法是( )
| A. | ①简单随机抽样,②系统抽样,③分层抽样 | |
| B. | ①简单随机抽样,②分层抽样,③系统抽样 | |
| C. | ①系统抽样,②简单随机抽样,③分层抽样 | |
| D. | ①分层抽样,②系统抽样,③简单随机抽样 |