题目内容
7.证明下列不等式:(1)$\sqrt{6}$+$\sqrt{7}$>$2\sqrt{2}+\sqrt{5}$
(2)${a}^{2}+{b}^{2}+3≥ab+\sqrt{3}(a+b)$.
分析 (1)采用分析法,两边平方,移项,即可证明不等式成;
(2)根据基本不等式的性质a2+b2≥2ab,${a^2}+3≥2\sqrt{3}a$,${b^2}+3≥2\sqrt{3}b$,以上各式相加即可求证不等式成立.
解答 证明:(1)要证不等式$\sqrt{6}$+$\sqrt{7}$>$2\sqrt{2}+\sqrt{5}$ 成立,
只需证($\sqrt{6}$+$\sqrt{7}$)2>(2$\sqrt{2}$+$\sqrt{5}$)2,------2
即证$2\sqrt{42}>2\sqrt{40}$,
即正$\sqrt{42}$>$\sqrt{40}$,
即42>40,-------------------------4
∵上式显然成立,
∴原不等式成立.------------------------------6
(2)∵a2+b2≥2ab,--------------8
${a^2}+3≥2\sqrt{3}a$,---------10
${b^2}+3≥2\sqrt{3}b$;
将此三式相加得
2$({a^2}+{b^2}+3)≥2ab+2\sqrt{3}a+2\sqrt{3}b$,
∴${a^2}+{b^2}+3≥ab+\sqrt{3}(a+b)$.--------12
点评 本题考查基本不等式的性质,考查“分析法”证明不等式成立,考查计算能力,属于中档题.

练习册系列答案
相关题目
19.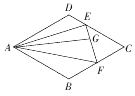 如图,在平行四边形ABCD中,$DE=\frac{1}{2}EC$,F为BC的中点,G为EF上的一点,且$\overrightarrow{AG}=m\overrightarrow{AB}+\frac{2}{3}\overrightarrow{AD}$,则实数m的值为( )
如图,在平行四边形ABCD中,$DE=\frac{1}{2}EC$,F为BC的中点,G为EF上的一点,且$\overrightarrow{AG}=m\overrightarrow{AB}+\frac{2}{3}\overrightarrow{AD}$,则实数m的值为( )
 如图,在平行四边形ABCD中,$DE=\frac{1}{2}EC$,F为BC的中点,G为EF上的一点,且$\overrightarrow{AG}=m\overrightarrow{AB}+\frac{2}{3}\overrightarrow{AD}$,则实数m的值为( )
如图,在平行四边形ABCD中,$DE=\frac{1}{2}EC$,F为BC的中点,G为EF上的一点,且$\overrightarrow{AG}=m\overrightarrow{AB}+\frac{2}{3}\overrightarrow{AD}$,则实数m的值为( )| A. | $\frac{7}{9}$ | B. | $-\frac{2}{9}$ | C. | $-\frac{1}{9}$ | D. | $\frac{5}{9}$ |
15.在用反证法证明“在△ABC中,若∠C是直角,则∠A和∠B都是锐角”的过程中,应该假设( )
| A. | ∠A和∠B都不是锐角 | B. | ∠A和∠B不都是锐角 | ||
| C. | ∠A和∠B都是钝角 | D. | ∠A和∠B都是直角 |
2.设a>b,c>d则下列不等式中一定成立的是( )
| A. | a+c>b+d | B. | ac>bd | C. | a-c>b-d | D. | a+d>b+c |
19.已知抛物线y2=2px(p>0)的焦点为F,P、Q是抛物线上的两点,若△FPQ是边长为2的正三角形,则p的值是( )
| A. | $2±\sqrt{3}$ | B. | $2+\sqrt{3}$ | C. | $\sqrt{3}±1$ | D. | $\sqrt{3}-1$ |