题目内容
11.若1弧度的圆心角所对的弧长为6,则这个圆心角所夹的扇形的面积是( )| A. | 3 | B. | 6 | C. | 18 | D. | 9 |
分析 由弧度的定义可求得扇形的半径,再由扇形的面积公式求解即可.
解答 解:由1弧度的圆心角所对的弧长为6,利用弧度定义得α=$\frac{l}{r}$,
所以r=6,
所以S=$\frac{1}{2}$lr=$\frac{1}{2}$•6•6=18.
故选:C.
点评 本题考查扇形的弧长公式和面积公式,属基础知识、基本运算的考查.

练习册系列答案
相关题目
19.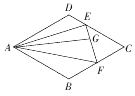 如图,在平行四边形ABCD中,$DE=\frac{1}{2}EC$,F为BC的中点,G为EF上的一点,且$\overrightarrow{AG}=m\overrightarrow{AB}+\frac{2}{3}\overrightarrow{AD}$,则实数m的值为( )
如图,在平行四边形ABCD中,$DE=\frac{1}{2}EC$,F为BC的中点,G为EF上的一点,且$\overrightarrow{AG}=m\overrightarrow{AB}+\frac{2}{3}\overrightarrow{AD}$,则实数m的值为( )
 如图,在平行四边形ABCD中,$DE=\frac{1}{2}EC$,F为BC的中点,G为EF上的一点,且$\overrightarrow{AG}=m\overrightarrow{AB}+\frac{2}{3}\overrightarrow{AD}$,则实数m的值为( )
如图,在平行四边形ABCD中,$DE=\frac{1}{2}EC$,F为BC的中点,G为EF上的一点,且$\overrightarrow{AG}=m\overrightarrow{AB}+\frac{2}{3}\overrightarrow{AD}$,则实数m的值为( )| A. | $\frac{7}{9}$ | B. | $-\frac{2}{9}$ | C. | $-\frac{1}{9}$ | D. | $\frac{5}{9}$ |
19.已知抛物线y2=2px(p>0)的焦点为F,P、Q是抛物线上的两点,若△FPQ是边长为2的正三角形,则p的值是( )
| A. | $2±\sqrt{3}$ | B. | $2+\sqrt{3}$ | C. | $\sqrt{3}±1$ | D. | $\sqrt{3}-1$ |
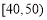 ,
,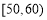 ,…,
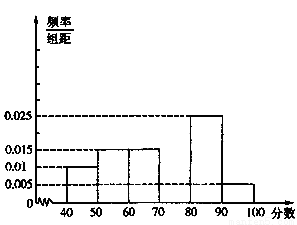
,…, 后画出如图的部分频率分布直方图,观察图形的信息,回答下列问题:
后画出如图的部分频率分布直方图,观察图形的信息,回答下列问题: