题目内容
11．已知随机变量X服从正态分布$N（6，\frac{1}{3}）$，则X的数学期望E（X）=6．分析 正态分布的性质得出答案．
解答 解：随机变量X服从正态分布$N（6，\frac{1}{3}）$，
∴μ=6，
故E（x）=6．
故答案为：6．
点评 本题考查了正态分布的数学期望，属于基础题．
练习册系列答案
备战中考寒假系列答案
相关题目
19．
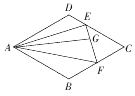如图，在平行四边形ABCD中，$DE=\frac{1}{2}EC$，F为BC的中点，G为EF上的一点，且$\overrightarrow{AG}=m\overrightarrow{AB}+\frac{2}{3}\overrightarrow{AD}$，则实数m的值为（ ）
如图，在平行四边形ABCD中，$DE=\frac{1}{2}EC$，F为BC的中点，G为EF上的一点，且$\overrightarrow{AG}=m\overrightarrow{AB}+\frac{2}{3}\overrightarrow{AD}$，则实数m的值为（ ）| A． | $\frac{7}{9}$ | B． | $-\frac{2}{9}$ | C． | $-\frac{1}{9}$ | D． | $\frac{5}{9}$ |
6．若函数f（x）=x3+x2+（a+6）x+a有极大值和极小值，则（ ）
| A． | $a＞-\frac{17}{3}$ | B． | $a≥-\frac{17}{3}$ | C． | $a＜-\frac{17}{3}$ | D． | $a≤-\frac{17}{3}$ |
15．在用反证法证明“在△ABC中，若∠C是直角，则∠A和∠B都是锐角”的过程中，应该假设（ ）
| A． | ∠A和∠B都不是锐角 | B． | ∠A和∠B不都是锐角 | ||
| C． | ∠A和∠B都是钝角 | D． | ∠A和∠B都是直角 |
2．设a＞b，c＞d则下列不等式中一定成立的是（ ）
| A． | a+c＞b+d | B． | ac＞bd | C． | a-c＞b-d | D． | a+d＞b+c |
19．已知抛物线y2=2px（p＞0）的焦点为F，P、Q是抛物线上的两点，若△FPQ是边长为2的正三角形，则p的值是（ ）
| A． | $2±\sqrt{3}$ | B． | $2+\sqrt{3}$ | C． | $\sqrt{3}±1$ | D． | $\sqrt{3}-1$ |
20．现要完成下列3项抽样调查：
①从10盒酸奶中抽取3盒进行食品卫生检查．
②科技报告厅有32排，每排有40个座位，有一次报告会恰好坐满了听众，报告会结束后，为了听取意见，
需要请32名听众进行座谈．
③高新中学共有160名教职工，其中一般教师120名，行政人员16名，后勤人员24名，为了了解教职工对学校在
校务公开方面的意见，拟抽取一个容量为20的样本．
较为合理的抽样方法是（ ）
①从10盒酸奶中抽取3盒进行食品卫生检查．
②科技报告厅有32排，每排有40个座位，有一次报告会恰好坐满了听众，报告会结束后，为了听取意见，
需要请32名听众进行座谈．
③高新中学共有160名教职工，其中一般教师120名，行政人员16名，后勤人员24名，为了了解教职工对学校在
校务公开方面的意见，拟抽取一个容量为20的样本．
较为合理的抽样方法是（ ）
| A． | ①简单随机抽样，②系统抽样，③分层抽样 | |
| B． | ①简单随机抽样，②分层抽样，③系统抽样 | |
| C． | ①系统抽样，②简单随机抽样，③分层抽样 | |
| D． | ①分层抽样，②系统抽样，③简单随机抽样 |