题目内容
4.(文)给出命题:①函数$y=cos(\frac{2}{3}x+\frac{7π}{2})$是奇函数;
②若α、β都是第一象限角且α<β,则tanα<tanβ;
③函数$y=2sin(\frac{2}{3}x+\frac{π}{3})$在区间$[-π,\frac{π}{2}]$上的最小值是-2,最大值是$\sqrt{3}$;
④直线$x=\frac{π}{8}$是函数$y=\frac{1}{2}sin(5x+\frac{7π}{8})$图象的一条对称轴.
其中正确命题的序号是①④.(写出所有正确命题的序号)
分析 ①根据诱导公式化简即可;
②根据正切函数图象分析;
③求出整体$\frac{2}{3}$x+$\frac{π}{3}$的范围,结合函数的图象得出最值;
④根据对称轴过函数的最值点判断即可.
解答 解:①函数$y=cos(\frac{2}{3}x+\frac{7π}{2})$=sin$\frac{2}{3}$x是奇函数,正确;
②若α、β都是第一象限角且α<β,由正切函数图象可知tanα<tanβ错误,比如tan60°>tan390°,故错误;
③函数$y=2sin(\frac{2}{3}x+\frac{π}{3})$,x∈$[-π,\frac{π}{2}]$,则$\frac{2}{3}$x+$\frac{π}{3}$∈[-$\frac{π}{3}$,$\frac{2π}{3}$],故最小值是-$\sqrt{3}$,最大值是2,故错误;
④直线$x=\frac{π}{8}$代入函数$y=\frac{1}{2}sin(5x+\frac{7π}{8})$=-$\frac{1}{2}$,成立,故是图象的一条对称轴.
故答案为①④.
点评 本题考查了三角函数图象的性质,属于基础题型,应熟练掌握.

练习册系列答案
相关题目
19.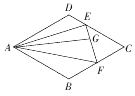 如图,在平行四边形ABCD中,$DE=\frac{1}{2}EC$,F为BC的中点,G为EF上的一点,且$\overrightarrow{AG}=m\overrightarrow{AB}+\frac{2}{3}\overrightarrow{AD}$,则实数m的值为( )
如图,在平行四边形ABCD中,$DE=\frac{1}{2}EC$,F为BC的中点,G为EF上的一点,且$\overrightarrow{AG}=m\overrightarrow{AB}+\frac{2}{3}\overrightarrow{AD}$,则实数m的值为( )
 如图,在平行四边形ABCD中,$DE=\frac{1}{2}EC$,F为BC的中点,G为EF上的一点,且$\overrightarrow{AG}=m\overrightarrow{AB}+\frac{2}{3}\overrightarrow{AD}$,则实数m的值为( )
如图,在平行四边形ABCD中,$DE=\frac{1}{2}EC$,F为BC的中点,G为EF上的一点,且$\overrightarrow{AG}=m\overrightarrow{AB}+\frac{2}{3}\overrightarrow{AD}$,则实数m的值为( )| A. | $\frac{7}{9}$ | B. | $-\frac{2}{9}$ | C. | $-\frac{1}{9}$ | D. | $\frac{5}{9}$ |
15.在用反证法证明“在△ABC中,若∠C是直角,则∠A和∠B都是锐角”的过程中,应该假设( )
| A. | ∠A和∠B都不是锐角 | B. | ∠A和∠B不都是锐角 | ||
| C. | ∠A和∠B都是钝角 | D. | ∠A和∠B都是直角 |