题目内容
若曲线y=
在点P(a,
)处的切线与两坐标轴围成的三角形的面积为2,则实数a的值是 .
| x |
| a |
考点:利用导数研究曲线上某点切线方程,直线的截距式方程
专题:导数的概念及应用,直线与圆
分析:求导数可得切线的斜率,进而可得切线的方程,可得其截距,由面积为2可得a的方程,解方程可得.
解答:
解:对y=
求导数可得y′=
,
∴曲线在P(a,
)处的切线斜率为k=
,
∴切线方程为:y-
=
(x-a),
令x=0,可得y=
,即直线的纵截距为
,
令y=0,可得x=-a,即直线的横截距为-a,
∴切线与两坐标轴围成的三角形的面积为:
S=
|
||-a|=2,解得a=4
故答案为:4
| x |
| 1 | ||
2
|
∴曲线在P(a,
| a |
| 1 | ||
2
|
∴切线方程为:y-
| a |
| 1 | ||
2
|
令x=0,可得y=
| ||
| 2 |
| ||
| 2 |
令y=0,可得x=-a,即直线的横截距为-a,
∴切线与两坐标轴围成的三角形的面积为:
S=
| 1 |
| 2 |
| ||
| 2 |
故答案为:4
点评:本题考查直线的截距,涉及导数法求曲线上某点的切线,属基础题.

练习册系列答案
 七彩题卡口算应用一点通系列答案
七彩题卡口算应用一点通系列答案
相关题目
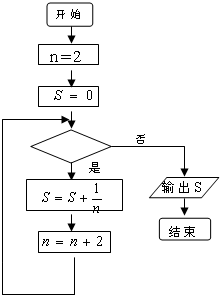
如图,这是计算
+
+
+…
的值的一个程序框图,其中判断框内填入的条件是( )
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 6 |
| 1 |
| 20 |

| A、n<20? |
| B、n<21? |
| C、n>19? |
| D、n>20? |
等比数列{an}满足,8a2+a5=0,则公比q=( )
| A、2 | B、-2 | C、±2 | D、3 |
 用一平面去截球所得截面的面积为3πcm2,已知球心到该截面的距离为1cm,则该球的体积是
用一平面去截球所得截面的面积为3πcm2,已知球心到该截面的距离为1cm,则该球的体积是