题目内容
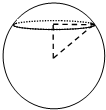用一平面去截球所得截面的面积为3πcm2，已知球心到该截面的距离为1cm，则该球的体积是考点：球的体积和表面积
专题：球
分析：求出小圆的半径，然后利用球心到该截面的距离为1 cm，小圆的半径，通过勾股定理求出球的半径，即可求出球的体积．
解答：
解：用一平面去截球所得截面的面积为3π cm2，∴小圆的半径为：
cm；
已知球心到该截面的距离为1 cm，∴球的半径为：
=2，
∴球的体积为：
×23=
π（cm3）
故答案为：
π．
| 3 |
已知球心到该截面的距离为1 cm，∴球的半径为：
12+(
|
∴球的体积为：
| 4π |
| 3 |
| 32 |
| 3 |
故答案为：
| 32 |
| 3 |
点评：本题是基础题，考查球的小圆的半径，球心到该截面的距离，球的半径之间的关系，满足勾股定理，考查计算能力．
练习册系列答案
相关题目
如果执行如图的程序框图，若输出的s=55，则k=（ ）
| A、8 | B、9 | C、10 | D、9或10 |
命题“存在x∈R，x3-x3+1＞0”的否定是（ ）
| A、不存在x∈R，x3-x3+1≤0 |
| B、存在x∈R，x3-x3+1≤0 |
| C、对任意的x∈R，x3-x3+1≤0 |
| D、对任意的x∈R，x3-x3+1＞0 |