题目内容
10.若m=0.52,n=20.5,p=log20.5,则( )| A. | n>m>p | B. | n>p>m | C. | m>n>p | D. | p>n>m |
分析 利用指数函数对数函数的运算性质即可得出.
解答 解:m=0.52=$\frac{1}{4}$,n=20.5=$\sqrt{2}$>1,p=log20.5=-1,
则n>m>p.
故选:A.
点评 本题考查了指数函数对数函数的运算性质,考查了推理能力与计算能力,属于基础题.

练习册系列答案
 小学教材全测系列答案
小学教材全测系列答案
相关题目
20.已知函数f(x)=$\frac{lnx}{x}$,关于x的不等式f2(x)+af(x)>0只有一个整数解,则实数a的取值范围是( )
| A. | (-$\frac{ln3}{3}$,-$\frac{ln2}{2}$] | B. | (-$\frac{1}{e}$,-$\frac{ln2}{2}$] | C. | [$\frac{ln2}{2}$,-$\frac{ln3}{3}$] | D. | [$\frac{ln2}{2}$,$\frac{1}{e}$) |
1.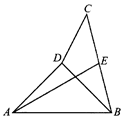 将正方形ABCD沿对角线BD折成直二面角后的图形如图所示,若E为线段BC的中点,则直线AE与平面ABD所成角的余弦为( )
将正方形ABCD沿对角线BD折成直二面角后的图形如图所示,若E为线段BC的中点,则直线AE与平面ABD所成角的余弦为( )
 将正方形ABCD沿对角线BD折成直二面角后的图形如图所示,若E为线段BC的中点,则直线AE与平面ABD所成角的余弦为( )
将正方形ABCD沿对角线BD折成直二面角后的图形如图所示,若E为线段BC的中点,则直线AE与平面ABD所成角的余弦为( )| A. | $\frac{1}{4}$ | B. | $\frac{{\sqrt{6}}}{6}$ | C. | $\frac{{\sqrt{30}}}{6}$ | D. | $\frac{{\sqrt{15}}}{4}$ |
2.已知点P在抛物线y2=x上,点Q在圆(x+$\frac{1}{2}$)2+(y-4)2=1上,则|PQ|的最小值为( )
| A. | $\frac{{3\sqrt{5}}}{2}-1$ | B. | $\frac{{3\sqrt{3}}}{2}-1$ | C. | $2\sqrt{3}-1$ | D. | $\sqrt{10}-1$ |
20.已知F1,F2是椭圆和双曲线的公共焦点,P是它们的一个公共点,且∠F1PF2=$\frac{π}{4}$,则椭圆和双曲线的离心率乘积的最小值为( )
| A. | $\frac{1}{2}$ | B. | $\frac{{\sqrt{2}}}{2}$ | C. | 1 | D. | $\sqrt{2}$ |
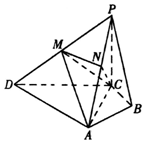 在四棱锥P-ABCD中,PC⊥底面ABCD,M,N分别是PD,PA的中点,AC⊥AD,∠ACD=∠ACB=60°,PC=AC.
在四棱锥P-ABCD中,PC⊥底面ABCD,M,N分别是PD,PA的中点,AC⊥AD,∠ACD=∠ACB=60°,PC=AC.