题目内容

5．已知双曲线C：$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1（a＞0，b＞0）的左顶点为A，点B（0，$\frac{\sqrt{15}}{3}$b），若线段AB的垂直平分线过右焦点F，则双曲线C的离心率为2．

分析 运用平面几何的性质可得AF=BF，由a，b，c的关系和离心率公式，计算即可得到所求值．

解答 解：∵线段AB的垂直平分线过右焦点F，∴BF=AF
$\sqrt{{c}^{2}+（\frac{\sqrt{15}}{3}b）^{2}}=a+c$，整理得5c2-6ac-8a2=0．
即5e2-6e-8=0，解得e=2，或e=-$\frac{4}{5}$（舍）．
∴双曲线C的离心率为2．
故答案为：2．

点评 本题考查双曲线的离心率的求法，注意运用平面几何的性质，以及双曲线的基本量的关系，考查运算能力，属中档题题．

练习册系列答案
相关题目
15．过抛物线C：y2=2px（p＞0）的焦点F作斜率为$\frac{4}{3}$的直线l与C及其准线分别相交于A、B、D三点，则$\frac{|AD|}{|BD|}$的值为（　　）
A．2或$\frac{1}{2}$B．3或$\frac{1}{3}$C．1D．4或$\frac{1}{4}$
16．已知角α的终边过点P（-4m，3m），（m＜0），则2sinα+cosα的值是$-\frac{2}{5}$．
13．已知椭圆C：$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1（a＞b＞0）的一个焦点与y2=4$\sqrt{3}$x的焦点重合，点$（\sqrt{3}，\frac{1}{2}）$在椭圆C上．
（1）求椭圆C的方程；
（2）设直线l：y=kx+m（k≠0）与椭圆C交于P，Q两点，且以PQ为对角线的菱形的一顶点为（-1，0），求△OPQ面积的最大值（O为坐标原点）．
20．已知椭圆C：$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1（a＞b＞0）$的一个焦点与${y^2}=4\sqrt{3}x$的焦点重合，点$（\sqrt{3}，\frac{1}{2}）$在椭圆C上．
（1）求椭圆C的方程；
（2）设直线l：y=kx+m（k≠0）与椭圆交于P，Q两点，且以PQ为对角线的菱形的一顶点为（-1，0），若$|PQ|=\frac{{2\sqrt{6}}}{3}$，求k的值．
10．若m=0.52，n=20.5，p=log20.5，则（　　）
A．n＞m＞pB．n＞p＞mC．m＞n＞pD．p＞n＞m
17．已知椭圆E：$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）的离心率是$\frac{\sqrt{3}}{2}$，点P（1，$\frac{\sqrt{3}}{2}$）在椭圆E上．
（1）求椭圆E的方程；
（2）过点P且斜率为k的直线l交椭圆E于点Q（xQ，yQ）（点Q异于点P），若0＜xQ＜1，求直线l斜率k的取值范围；
（3）若以点P为圆心作n个圆Pi（i=1，2，…，n），设圆Pi交x轴于点Ai、Bi，且直线PAi、PBi分别与椭圆E交于Mi、Ni（Mi、Ni皆异于点P），证明：M1N1∥M2N2∥…∥MnNn．
14．已知向量$\overrightarrow{m}$=（sinx，-1），$\overrightarrow{n}$=（cosx，$\frac{3}{2}$），函数f（x）=（$\overrightarrow{m}$+$\overrightarrow{n}$）•$\overrightarrow{m}$．
（1）求函数f（x）的单调递增区间；
（2）将函数f（x）的图象向左平移$\frac{π}{8}$个单位得到函数g（x）的图象，在△ABC中，角A，B，C所对边分别a，b，c，若a=3，g（$\frac{A}{2}$）=$\frac{\sqrt{6}}{6}$，sinB=cosA，求b的值．
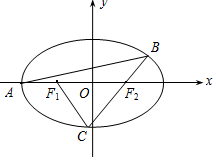15．如图，已知椭圆E：$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）的左顶点A（-2，0），且点（-1，$\frac{3}{2}$）在椭圆上，F1、F2分别是椭圆的左、右焦点．过点A作斜率为k（k＞0）的直线交椭圆E于另一点B，直线BF2交椭圆E于点C．
（1）求椭圆E的标准方程；
（2）若△CF1F2为等腰三角形，求点B的坐标；
（3）若F1C⊥AB，求k的值．
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网