题目内容
20.已知F1,F2是椭圆和双曲线的公共焦点,P是它们的一个公共点,且∠F1PF2=$\frac{π}{4}$,则椭圆和双曲线的离心率乘积的最小值为( )| A. | $\frac{1}{2}$ | B. | $\frac{{\sqrt{2}}}{2}$ | C. | 1 | D. | $\sqrt{2}$ |
分析 设椭圆的长半轴长为a1,双曲线的半实轴长a2,焦距2c.由椭圆及双曲线定义用a1,a2表示出|PF1|,|PF2|,在△F1PF2中根据余弦定理可得到a1,a2与c的关系,转化为离心率,再由基本不等式得结论.
解答 解:如图,设椭圆的长半轴长为a1,双曲线的半实轴长为a2,则根据椭圆及双曲线的定义:
|PF1|+|PF2|=2a1,|PF1|-|PF2|=2a2,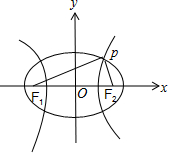
∴|PF1|=a1+a2,|PF2|=a1-a2,
设|F1F2|=2c,∠F1PF2=$\frac{π}{4}$,则:
在△PF1F2中由余弦定理得,
4c2=(a1+a2)2+(a1-a2)2-2(a1+a2)(a1-a2)cos$\frac{π}{4}$,
化简得:($2-\sqrt{2}$)a12+($2+\sqrt{2}$)a22=4c2,
即$\frac{2-\sqrt{2}}{{{e}_{1}}^{2}}+\frac{2+\sqrt{2}}{{{e}_{2}}^{2}}=4$,
又∵$\frac{2-\sqrt{2}}{{{e}_{1}}^{2}}+\frac{2+\sqrt{2}}{{{e}_{2}}^{2}}≥\frac{2\sqrt{{2}^{2}-2}}{{e}_{1}•{e}_{2}}=\frac{2\sqrt{2}}{{e}_{1}•{e}_{2}}$,
∴$\frac{2\sqrt{2}}{{e}_{1}•{e}_{2}}≤4$,即e1•e2≥$\frac{\sqrt{2}}{2}$,
即椭圆和双曲线的离心率乘积的最小值为$\frac{\sqrt{2}}{2}$.
故选:B.
点评 本题考查圆锥曲线的共同特征,考查通过椭圆与双曲线的定义求焦点三角形三边长,解决本题的关键是根据所得出的条件灵活变形,求出焦点三角形的边长来,是中档题.

 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案| A. | n>m>p | B. | n>p>m | C. | m>n>p | D. | p>n>m |
| A. | $\frac{5\sqrt{2}}{13}$ | B. | $\frac{12}{13}$ | C. | $\frac{7\sqrt{2}}{26}$ | D. | $\frac{17\sqrt{2}26}{\;}$ |
| A. | a≥0 | B. | b≤0 | C. | c=0 | D. | a-2b+c=0 |
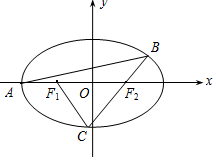 如图,已知椭圆E:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左顶点A(-2,0),且点(-1,$\frac{3}{2}$)在椭圆上,F1、F2分别是椭圆的左、右焦点.过点A作斜率为k(k>0)的直线交椭圆E于另一点B,直线BF2交椭圆E于点C.
如图,已知椭圆E:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左顶点A(-2,0),且点(-1,$\frac{3}{2}$)在椭圆上,F1、F2分别是椭圆的左、右焦点.过点A作斜率为k(k>0)的直线交椭圆E于另一点B,直线BF2交椭圆E于点C.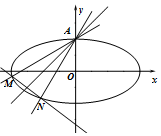 如图,已知直线l:y=kx+1(k>0)关于直线y=x+1对称的直线为l1,直线l,l1与椭圆E:$\frac{x^2}{4}+{y^2}$=1分别交于点A、M和A、N,记直线l1的斜率为k1.
如图,已知直线l:y=kx+1(k>0)关于直线y=x+1对称的直线为l1,直线l,l1与椭圆E:$\frac{x^2}{4}+{y^2}$=1分别交于点A、M和A、N,记直线l1的斜率为k1.