题目内容
已知目标函数z=ax+by(a>0,b>0)在约束条件
下的最大值为3,则代数式
+
的最小值为( )
|
| 1 |
| 1-a |
| 4 |
| 1-b |
| A、10 | B、9 | C、8 | D、7 |
考点:简单线性规划
专题:数形结合
分析:由约束条件作出可行域,由图得到使目标函数z=ax+by(a>0,b>0)取得最大值的点,解出点的坐标,代入目标函数得到a+b=1,进一步代入
+
后利用基本不等式求最值.
| 1 |
| 1-a |
| 4 |
| 1-b |
解答:
 解:由约束条件
解:由约束条件
作可行域如图,
由图可知,当目标函数z=ax+by过可行域内的点C时,z有最大值.
联立
,解得:
.
∴C(3,3).
则3a+3b=3,即a+b=1(a>0,b>0).
∴
+
=
+
=(
+
)(a+b)=5+
+
≥5+2
=9.
当且仅当
,即a=
,b=
时上式等号成立.
故选:B.
 解:由约束条件
解:由约束条件
|
由图可知,当目标函数z=ax+by过可行域内的点C时,z有最大值.
联立
|
|
∴C(3,3).
则3a+3b=3,即a+b=1(a>0,b>0).
∴
| 1 |
| 1-a |
| 4 |
| 1-b |
| 1 |
| b |
| 4 |
| a |
| 1 |
| b |
| 4 |
| a |
| a |
| b |
| 4b |
| a |
≥5+2
|
当且仅当
|
| 2 |
| 3 |
| 1 |
| 3 |
故选:B.
点评:本题考查了简单的线性规划,考查了数形结合的解题思想方法,训练了利用基本不等式求最值,是中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
定义一种运算a?b=
,令f(x)=(3+2x-x2)?|x-t|(t为常数),且x∈[-3,3],则使函数f(x)的最大值为3的t的集合是( )
|
| A、{3,-3} |
| B、{-1,5} |
| C、{3,-1} |
| D、{-3,-1,3,5} |
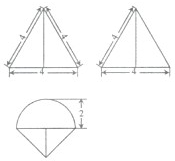
某简单组合体的三视图如图所示,则该组合体的体积为( )

A、
| ||||||
B、
| ||||||
C、
| ||||||
D、
|
若不等式2kx2+kx-
≥0的解集为空集,则实数k的取值范围是( )
| 3 |
| 8 |
| A、(-3,0) |
| B、(-∞,-3) |
| C、(-3,0] |
| D、(-∞,-3)∪(0,+∞) |
已知集合A={x|x2<4x},集合B={y|y=-x2,-1≤x≤2},则集合∁R(A∩B)=( )
| A、R | B、{0} |
| C、∅ | D、{x|x≥4或x≤0} |
已知复数z=2+i,
是z的共轭复数,则
对应的点位于( )
. |
| z |
| ||
| z |
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
在(2
-
)5的二项展开式中,x的系数为( )
| x |
| 1 |
| x |
| A、-80 | B、-5 | C、10 | D、80 |
 正方体两条棱的中点分别为M、N,它被平面AMN及平面DNC1截去两个角后所得的几何体如图,则该几何体的正视图为( )
正方体两条棱的中点分别为M、N,它被平面AMN及平面DNC1截去两个角后所得的几何体如图,则该几何体的正视图为( )


