题目内容
已知命题：“?x∈[-2，1]，使x2+2x+a≥0”为真命题，则a的取值范围是 ．
考点：全称命题
专题：简易逻辑
分析：求出x∈[-2，1]，x2+2x的最小值，然后利用命题是真命题即可求出a的范围．
解答：
解：x∈[-2，1]，y=x2+2x的对称轴是x=-1，表达式的最小值为：a-1．
“?x∈[-2，1]，使x2+2x+a≥0”为真命题，
∴a≥1．
故答案为：{a|a≥1}．
“?x∈[-2，1]，使x2+2x+a≥0”为真命题，
∴a≥1．
故答案为：{a|a≥1}．
点评：本题考查命题的真假的判断与应用，二次函数的最值问题．
练习册系列答案
冲刺100分1号卷系列答案
期末好成绩系列答案
相关题目
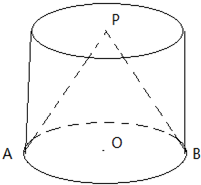已知一个圆柱和一个圆锥等底等高，如图，点O为底面的圆心，点P为圆锥的顶点．若圆柱的高等于它的底面直径．