题目内容
已知tanα=2,则
= .
| 6sinα+cosα |
| 3sinα-2cosα |
考点:同角三角函数基本关系的运用
专题:三角函数的求值
分析:原式分子分母除以cosα,利用同角三角函数间基本关系变形,将tanα的值代入计算即可求出值.
解答:
解:∵tanα=2,
∴原式=
=
=
.
故答案为:
∴原式=
| 6tanα+1 |
| 3tanα-2 |
| 6×2+1 |
| 3×2-2 |
| 13 |
| 4 |
故答案为:
| 13 |
| 4 |
点评:此题考查了同角三角函数基本关系的运用,熟练掌握基本关系是解本题的关键.

练习册系列答案
 一线名师权威作业本系列答案
一线名师权威作业本系列答案
相关题目
已知奇函数y=f(x)在区间[-b,-a]上为减函数,且在此区间上,y=f(x)的最小值为2,则函数y=|f(x)|在区间[a,b]上是( )
| A、增函数且最大值为2 |
| B、增函数且最小值为2 |
| C、减函数且最大值为2 |
| D、减函数且最小值为2 |
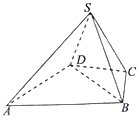 已知在四棱锥S-ABCD中,△ABD为正三角形,CB=CD,∠DCB=120°,SD=SB,
已知在四棱锥S-ABCD中,△ABD为正三角形,CB=CD,∠DCB=120°,SD=SB, 如图是甲、乙两名同学三次测验成绩的茎叶图,则甲、乙两名同学中成绩更稳定的是
如图是甲、乙两名同学三次测验成绩的茎叶图,则甲、乙两名同学中成绩更稳定的是