题目内容
第七届国际数学教育大会的会徽的主体是由一连串直角三角形演变而成,其中OA=AB=BC=CD=DE=EF=FG=GH=HI=1,若将图2的直角三角形继续作下去,并记OA、OB、…、OI、…的长度所构成的数列为{an}.

(1)求数列{an}的通项公式;
(2)若数列bn=
的前n项和Sn,Sn.

(1)求数列{an}的通项公式;
(2)若数列bn=
| 1 |
| an+1+an |
考点:数列的求和,归纳推理
专题:等差数列与等比数列
分析:(1)根据条件确定an满足的关系式,构造等差数列即可求数列{an}的通项公式;
(2)求出bn的通项公式,利用分母有理化,进行求和.
(2)求出bn的通项公式,利用分母有理化,进行求和.
解答:
解:(1)∵OA=AB=BC=CD=DE=EF=FG=GH=HI=1,
∴a22=a12+1,a32=a22+1,…
=
+1,
即数列{
}是以1为首项,1为公差的等差数列,则
=1+(n-1)=n,
即an=
.
(2)bn=
=
=
-
,
则Sn=(
-1)+(
-
)+…+
-
=
-1.
∴a22=a12+1,a32=a22+1,…
| a | 2 n+1 |
| a | 2 n |
即数列{
| a | 2 n |
| a | 2 n |
即an=
| n |
(2)bn=
| 1 |
| an+1+an |
| 1 | ||||
|
| n+1 |
| n |
则Sn=(
| 2 |
| 3 |
| 2 |
| n+1 |
| n |
| n+1 |
点评:本题主要考查等差数列的判定和应用,以及利用分母有理化进行数列求和,考查学生的计算能力.

练习册系列答案
相关题目
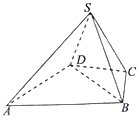 已知在四棱锥S-ABCD中,△ABD为正三角形,CB=CD,∠DCB=120°,SD=SB,
已知在四棱锥S-ABCD中,△ABD为正三角形,CB=CD,∠DCB=120°,SD=SB, 已知函数f(x)=3sin(2x-
已知函数f(x)=3sin(2x-