题目内容

在△ABC中，角A，B，C的对边分别为a，b，c，若△ABC的面积S=2
3
，b=4，A=
π
3
，求BC边的长．
考点：正弦定理
专题：解三角形
分析：利用三角形的面积计算公式、余弦定理即可得出．
解答： 解：∵S=2
3
，b=4，A=
π
3
，
∴S=
1
2
bcsinA，
∴2
3
=
1
2
×4csin
π
3
，
解得c=2．
∴a2=b2+c2-2bccosA=42+22-2×4×2×cos
π
3
=12，
解得a=2
3
．
点评：本题考查了三角形的面积计算公式、余弦定理，考查了推理能力与计算能力，属于中档题．
练习册系列答案
相关题目
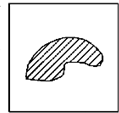如图，边长为2的正方形有一封闭曲线围成的阴影区域，在正方形中随机撒一粒豆子，它落在阴影区域内的概率为
2
3
，则阴影区域的面积为（　　）
A、
2
3
B、
4
3
C、
8
3
D、无法计算
计算：（1+
1
2
+
1
3
+
1
4
+…+
1
201404
）2+（
1
2
+
1
3
+
1
4
+…+
1
201404
）2+（
1
3
+
1
4
+…+
1
201404
）2+…+（
1
201404
）2+（1+
1
2
+
1
3
+
1
4
+…+
1
201404
）．
若函数f（x）=x2+ax+a2的最小值为3，则常数a=
 
．
已知tanα=
1
7
，tanβ=
3
4
，且α，β都是锐角，求α+β的值．
已知x，y∈R，且满足
x2-4x+4+y2
=
1
2
|x+y-2|，试判断点M的轨迹是怎样的曲线．
下列关系式，正确的是（　　）
A、（
1
3
）-2＜（
1
3
）2
B、log 
2
3
3
2
＜log 
1
3
2
C、0.52.3＞0.62.3
D、log34＜log0.30.4
函数f（x）=3sin
π
2
x+log2x的零点个数是（　　）
A、1B、3C、4D、5
等差数列{an}中，an＞0，且a1+a3+a8=a42，则S7=
 
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网