题目内容
函数f(x)=3sin
x+log2x的零点个数是( )
| π |
| 2 |
| A、1 | B、3 | C、4 | D、5 |
考点:函数零点的判定定理
专题:函数的性质及应用
分析:转化为:y=-3sin
与y=log
图象的交点个数,画出图象即可判断.
| πx |
| 2 |
x 2 |
解答:
解:∵函数f(x)=3sin
x+log2x,
∴转化为:y=-3sin
与y=log
图象的交点个数,

根据图象判断:有5个交点个数,
故选:D
| π |
| 2 |
∴转化为:y=-3sin
| πx |
| 2 |
x 2 |

根据图象判断:有5个交点个数,
故选:D
点评:本题考查了函数的图象,运用图象解决函数交点个数问题,零点个数问题,属于中档题.

练习册系列答案
 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案
相关题目
已知各项均为正数的等比数列{an}满足a1a2a3a4=6,a7a8a9a10=6
,则a13a14a15a16=( )
| 3 |
| A、18 | ||
B、10
| ||
| C、10 | ||
D、
|
把边长为2的正三角形ABC沿BC边上的高AD折成直二面角,设折叠后BC中点为M,则AC与DM所成角的余弦值为
( )
( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
 如图所示,已知在四棱锥P-ABCD中,CD∥AB,AD⊥AB,BC⊥PC,且AD=DC=PA=
如图所示,已知在四棱锥P-ABCD中,CD∥AB,AD⊥AB,BC⊥PC,且AD=DC=PA=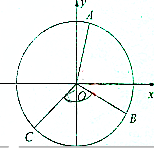 如图,在平面直角坐标系xOy中,单位圆上的A、B两点分别在第一、四象限,已知A、B两点的纵坐标分别为
如图,在平面直角坐标系xOy中,单位圆上的A、B两点分别在第一、四象限,已知A、B两点的纵坐标分别为