题目内容

已知x，y∈R，且满足
x2-4x+4+y2
=
1
2
|x+y-2|，试判断点M的轨迹是怎样的曲线．
考点：曲线与方程
专题：计算题,圆锥曲线的定义、性质与方程
分析：由题意，
(x-2)2+(y-0)2
|x+y-2|
2
=
2
2
，可得（x，y）到（2，0）的距离与到直线x+y-2=0的距离的比为
2
2
，即可得出结论．
解答： 解：由题意，
(x-2)2+(y-0)2
|x+y-2|
2
=
2
2
，
∴（x，y）到（2，0）的距离与到直线x+y-2=0的距离的比为
2
2
，
利用椭圆的定义，可得轨迹是椭圆．
点评：本题考查曲线与方程，考查椭圆的定义，正确变形是关键．
练习册系列答案
相关题目
下列命题中，其中是假命题的为（　　）
①若m，n是异面直线，且m⊥α，n⊥β，则α与β不会平行；
②函数f（x）=|cos2x-1|的最小正周期是π；
③命题“?a∈R，函数f（x）=（x-1）a+1恒过定点（1，1）”为真；
④“命题p∨q为真”是“命题p∧q为真”的必要不充分条件．
A、0个B、1个C、2个D、3个
若
a
•
b
=-10，|
a
|=5，|
b
|=4，则
a
，
b
的夹角为
 
．
某种波的传播是由曲线f（x）=Asin（ωx+φ）（A＞0）来实现的，我们把函数解析式f（x）=Asin（ωx+φ）称为“波”，把振幅都是A 的波称为“A 类波”，把两个解析式相加称为波的叠加．
（1）已知“1 类波”中的两个波f1（x）=sin（x+φ1）与f2（x）=sin（x+φ2）叠加后仍是“1类波”，求φ2-φ1的值；
（2）在“A 类波“中有一个是f1（x）=Asinx，从 A类波中再找出两个不同的波f2（x），f3（x），使得这三个不同的波叠加之后是平波，即叠加后f1（x）+f2（x）+f3（x），并说明理由．
（3）在n（n∈N，n≥2）个“A类波”的情况下对（2）进行推广，使得（2）是推广后命题的一个特例．只需写出推广的结论，而不需证明．
在△ABC中，角A，B，C的对边分别为a，b，c，若△ABC的面积S=2
3
，b=4，A=
π
3
，求BC边的长．
设平面α与平面β相交于直线m，直线a在平面α内，直线b在平面β内，且b⊥m，则“α⊥β”是“a⊥b”的（　　）
A、必要不充分条件
B、充分不必要条件
C、充分必要条件
D、既不充分也不必要条件
已知|z1|=|z2|=1，z1+z2=
1
2
+
3
2
i，求复数z1、z2及|z1-z2|．
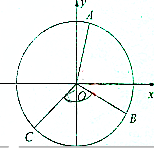如图，在平面直角坐标系xOy中，单位圆上的A、B两点分别在第一、四象限，已知A、B两点的纵坐标分别为
7
2
10
，-
5
5
．
（1）求tan∠AOB的值；
（2）设点A关于直线OB的对称点为C，求C点坐标．
设集合M={0，1，2}，N={x|x2-5x+6≤0}，则M∩N=
 
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网