题目内容
已知正项数列{an}满足a1=1，a2=2，2an2=an-12+an+12（n≥2），则a2013= ．
考点：数列的求和
专题：等差数列与等比数列
分析：由已知条件推导出∴{an2}是首项为1，公差为3的等差数列，由此能求出a2013=
．
| 6037 |
解答：
解：∵2an2=an-12+an+12（n≥2），a1=1，a2=2，
∴a22-a12=4-1=3，a12=1，
∴{an2}是首项为1，公差为3的等差数列，
∴a20132=1+2012×3=6037，
∴a2013=
．
故答案为：
．
∴a22-a12=4-1=3，a12=1，
∴{an2}是首项为1，公差为3的等差数列，
∴a20132=1+2012×3=6037，
∴a2013=
| 6037 |
故答案为：
| 6037 |
点评：本题考查数列的前n项和的求法，解题时要认真审题，注意等差数列的性质的灵活运用．
练习册系列答案
相关题目
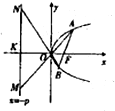如图，过抛物线C：y2=2px的焦点F与x轴不垂直的直线交抛物线C与A、B两点，直线AO、BO分别与直线m：x=-p相交于M、N两点，则