题目内容
某产品的销售收入y1（万元）是产量x（千台）的函数，y1=17x2；生产总成本y2（万元）也是x的函数，y2=2x3-x2（x＞0），为使利润最大，应生产 千台．
考点：函数解析式的求解及常用方法,基本不等式
专题：应用题,导数的概念及应用
分析：根据题意，列出利润函数，利用导数求出利润函数在何时取得最大值即可．
解答：
解：根据题意，利润函数为
y=y1-y2=17x2-（2x3-x2）=-2x3+18x2（x＞0）；
对函数求导，得
y′=-6x2+36x；
令y′=0，
解得x=0，或x=6；
∴当x∈（0，6）时，y′＞0，y是增函数；
当x∈（6，+∞）时，y′＜0，y是减函数；
∴当x=6时，y取得最大值．
所以，为使利润最大，应生产6千台．
故答案为：6．
y=y1-y2=17x2-（2x3-x2）=-2x3+18x2（x＞0）；
对函数求导，得
y′=-6x2+36x；
令y′=0，
解得x=0，或x=6；
∴当x∈（0，6）时，y′＞0，y是增函数；
当x∈（6，+∞）时，y′＜0，y是减函数；
∴当x=6时，y取得最大值．
所以，为使利润最大，应生产6千台．
故答案为：6．
点评：本题考查了利用导数研究函数最值的应用问题，解题时应根据题意，列出目标函数，利用导数研究函数的单调性与最值，是中档题．
练习册系列答案
相关题目
若α，β∈（0，
），sin（α-
）=
，sin（
-β）=-
，则cos（α+β）的值等于（ ）
| π |
| 2 |
| β |
| 2 |
| 1 |
| 2 |
| α |
| 2 |
| 1 |
| 2 |
A、-
| ||||
B、-
| ||||
C、
| ||||
D、
|
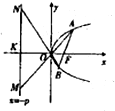如图，过抛物线C：y2=2px的焦点F与x轴不垂直的直线交抛物线C与A、B两点，直线AO、BO分别与直线m：x=-p相交于M、N两点，则