题目内容
在极坐标系中,直线ρsin(θ+
)=2,被圆ρ=3截得的弦长为( )
| π |
| 4 |
A、2
| ||
| B、2 | ||
C、2
| ||
D、2
|
考点:简单曲线的极坐标方程
专题:坐标系和参数方程
分析:把极坐标方程化为直角坐标方程,利用点到直线的距离公式求出弦心距,再利用弦长公式求得弦长.
解答:
解:直线ρsin(θ+
)=2,即
ρcosθ+
ρsinθ=2,
化为直角坐标方程为 x+y-2
=0,
圆ρ=3 即 x2+y2=9,表示以原点为圆心、半径等于3的圆.
弦心距d=
=2,可得弦长为 2
=2
=2
,
故选:C.
| π |
| 4 |
| ||
| 2 |
| ||
| 2 |
化为直角坐标方程为 x+y-2
| 2 |
圆ρ=3 即 x2+y2=9,表示以原点为圆心、半径等于3的圆.
弦心距d=
|0+0-2
| ||
|
| r2-d2 |
| 9-4 |
| 5 |
故选:C.
点评:本题主要考查把极坐标方程化为直角坐标方程的方法,点到直线的距离公式的应用,直线和圆的位置关系,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
若α,β∈(0,
),sin(α-
)=
,sin(
-β)=-
,则cos(α+β)的值等于( )
| π |
| 2 |
| β |
| 2 |
| 1 |
| 2 |
| α |
| 2 |
| 1 |
| 2 |
A、-
| ||||
B、-
| ||||
C、
| ||||
D、
|
函数f(x)=x3+x在实数范围内( )
| A、单调递增 | B、单调递减 |
| C、先增后减 | D、先减后增 |
双曲线5x2+ky2=5的一个焦点是(
,0),那么实数k的值为( )
| 6 |
| A、-25 | B、25 | C、-1 | D、1 |
已知m,n是不同的直线,α,β是不重合的平面,下列命题正确的是( ):
| A、若m∥α,则m平行于平面α内的任意一条直线 |
| B、若α∥β,m?α,n?β,则m∥n |
| C、若α∥β,m?α,则m∥β. |
| D、若m?α,n?α,m∥β,n∥β,则α∥β |
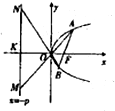 如图,过抛物线C:y2=2px的焦点F与x轴不垂直的直线交抛物线C与A、B两点,直线AO、BO分别与直线m:x=-p相交于M、N两点,则
如图,过抛物线C:y2=2px的焦点F与x轴不垂直的直线交抛物线C与A、B两点,直线AO、BO分别与直线m:x=-p相交于M、N两点,则




