题目内容
若tan(
-α)=3,则tan2α=( )
| π |
| 4 |
A、-
| ||
B、
| ||
C、-
| ||
D、
|
考点:两角和与差的正切函数,二倍角的正切
专题:三角函数的求值
分析:由题意和两角和与差的正切函数可的tanα,再由二倍角的正切公式可得tan2α
解答:
解:∵tan(
-α)=3,
∴tanα=tan[
-(
-α)]
=
=-
,
∴tan2α=
=-
故选:C
| π |
| 4 |
∴tanα=tan[
| π |
| 4 |
| π |
| 4 |
=
1-tan(
| ||
1+tan(
|
| 1 |
| 2 |
∴tan2α=
| 2tanα |
| 1-tan2α |
| 4 |
| 3 |
故选:C
点评:本题考查两角和与差的正切函数,涉及二倍角的正切公式,属基础题.

练习册系列答案
相关题目
函数y=
的图象大致是( )
| x3 |
| 3x-1 |
A、 |
B、 |
C、 |
D、 |
若0<a<1且b>1,则函数y=ax-b的图象不经过( )
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
 如图,四边形ABCD为正方形,PD⊥平面ABCD,∠DPC=30°,AF⊥PC于点F,FE∥CD交PD于点E.
如图,四边形ABCD为正方形,PD⊥平面ABCD,∠DPC=30°,AF⊥PC于点F,FE∥CD交PD于点E.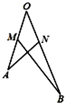 如图,M、N分别是线段OA、OB上的点,OM=MA=ON=1,NB=2,设
如图,M、N分别是线段OA、OB上的点,OM=MA=ON=1,NB=2,设