Question

11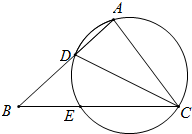．如图，在△ABC中，CD是∠ACB的平分线，△ACD的外接圆交BC于点E，AC=CE=3，AB=4，则AD 的长为（　　）

• A． $\frac{3}{2}$
• B． 2
• C． $\frac{5}{2}$
• D． 3

Answer 1

分析 连接DE，因为ACED是圆的内接四边形，所以△BDE∽△BCA，由此能够证明BE=$\frac{4}{3}$DA，根据割线定理得BD•BA=BE•BC，即（AB-AD）•BA=$\frac{4}{3}$DA•（$\frac{4}{3}$DA+CE），由此能求出AD．

解答 解：连接DE，
∵ACED是圆的内接四边形，
∴∠BDE=∠BCA，
∵∠DBE=∠CBA，
∴△BDE∽△BCA，
∴$\frac{BE}{BA}=\frac{DE}{CA}$．
∵CD是∠ACB的平分线，∴AD=DE，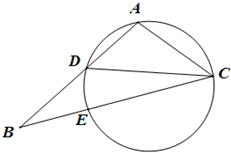
∵AC=CE=3，AB=4，
∴4DA=3BE，即BE=$\frac{4}{3}$DA，
设AD=DE=t，则BE=$\frac{4}{3}$t，
根据割线定理得BD•BA=BE•BC，
∴（AB-AD）•BA=$\frac{4}{3}$DA•（$\frac{4}{3}$DA+CE），
∴（4-t）×4=$\frac{4}{3}$t（$\frac{4}{3}$t+3），
∴2t²+9t-18=0，
解得t=$\frac{3}{2}$，或t=-6（舍），即AD=$\frac{3}{2}$．
故选：A．

点评 本题考查与圆有关的比例线段的应用，是中档题．解题时要认真审题，仔细解答，注意圆的内接四边形的性质和切割线定理的合理运用．