题目内容
19.已知圆O:x2+y2=4,点F($\sqrt{3}$,0),以线段MF为直径的圆内切于圆O,记点M的轨迹为C(1)求曲线C的方程;
(2)若过F的直线l与曲线C交于A,B两点,问:在x轴上是否存在点N,使得$\overrightarrow{NA}$•$\overrightarrow{NB}$为定值?若存在,求出点N坐标;若不存在,说明理由.
分析 (1)设FM的中点为Q,切点为G,连OQ,QG,通过|OQ|+|QG|=|OG|=2,推出|F′M|+|MF|=4.说明点M的轨迹是以F′,F为焦点,长轴长为4的椭圆.然后求解曲线C的方程;
(2)当直线l的斜率存在时,设其方程为y=k(x-$\sqrt{3}$),联立直线方程和椭圆方程,利用根与系数的关系得到A,B的横坐标的和与积,代入$\overrightarrow{NA}$•$\overrightarrow{NB}$,由$\overrightarrow{NA}$•$\overrightarrow{NB}$为定值求得m值,验证斜率不存在时适合得答案.
解答 解:(1)设FM的中点为Q,切点为G,连OQ,QG,
则|OQ|+|QG|=|OG|=2,取F关于y轴的对称点F′,连F′M,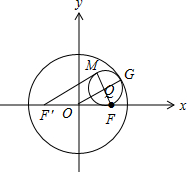
故|F′M|+|MF|=2(|OQ|+|QG|)=4.
点M的轨迹是以F′,F为焦点,长轴长为4的椭圆.
其中,a=2,c=,b=1,则曲线C的方程为$\frac{{x}^{2}}{4}$+y2=1;
(2)当直线l的斜率存在时,设其方程为y=k(x-$\sqrt{3}$),
A(x1,y1),B(x2,y2),
联立$\left\{\begin{array}{l}{y=k(x-\sqrt{3})}\\{\frac{{x}^{2}}{4}+{y}^{2}=1}\end{array}\right.$,得$(1+4{k}^{2}){x}^{2}-8\sqrt{3}{k}^{2}x+12{k}^{2}-4=0$.
则△>0,${x}_{1}+{x}_{2}=\frac{8\sqrt{3}{k}^{2}}{1+4{k}^{2}},{x}_{1}{x}_{2}=\frac{12{k}^{2}-4}{1+4{k}^{2}}$,
若存在定点N(m,0)满足条件,
则有$\overrightarrow{NA}•\overrightarrow{NB}$=(x1-m)(x2-m)+y1y2
=x1x2+${m}^{2}-m({x}_{1}+{x}_{2})+{k}^{2}({x}_{1}-\sqrt{3})({x}_{2}-\sqrt{3})$
=$(1+{k}^{2}){x}_{1}{x}_{2}-(m+\sqrt{3}{k}^{2})({x}_{1}+{x}_{2})+3{k}^{2}+{m}^{2}$
=$(1+{k}^{2})\frac{12{k}^{2}-4}{1+4{k}^{2}}-(m+\sqrt{3}{k}^{2})\frac{8\sqrt{3}{k}^{2}}{1+4{k}^{2}}+3{k}^{2}+{m}^{2}$=$\frac{(4{m}^{2}-8\sqrt{3}m+11){k}^{2}+{m}^{2}-4}{4{k}^{2}+1}$.
如果要上式为定值,则必须有$\frac{4{m}^{2}-8\sqrt{3}m+11}{{m}^{2}-4}=4$,解得m=$\frac{9\sqrt{3}}{8}$,
此时$\overrightarrow{NA}•\overrightarrow{NB}$=${m}^{2}-4=-\frac{13}{64}$.
验证当直线l斜率不存在时,也符合.
故存在点N($\frac{9\sqrt{3}}{8}$,0)满足$\overrightarrow{NA}$•$\overrightarrow{NB}$为定值.
点评 本题考查椭圆方程的求法,考查满足条件的点是否存在的判断与求法,是中档题,解题时要认真审题,注意韦达定理、根的判别式、向量的数量积、椭圆性质的合理运,是中档题.

 同步练习强化拓展系列答案
同步练习强化拓展系列答案| A. | 真命题,真命题 | B. | 真命题,假命题 | C. | 假命题,真命题 | D. | 假命题,假命题 |
成绩记录如表所示:
| 队员编号 | 1 | 2 | 3 | 4 | 5 |
| 甲班成绩 | 31 | 34 | 33 | 29 | 28 |
| 乙班成绩 | 27 | 31 | 30 | X | 31 |
(1)若x=36,从甲班的5名同学中任取3名,记这3人中用时少于乙队平均用时的人数为随机变量η,求η的分布列;
(2)若最终乙班获胜,那么当乙班同学的成绩方差最大时,x的取值是多少(直接写出结果,不用证明)?
| A. | $\frac{1}{2}$ | B. | $\frac{1}{2e^2}$-1 | C. | $\frac{1}{2e^2}$+1 | D. | $\frac{e^2}{2}$-1 |
| A. | {0,2,3} | B. | {0,3,5} | C. | {0,1,2,3} | D. | {0,2,3,5} |
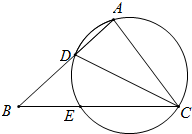 如图,在△ABC中,CD是∠ACB的平分线,△ACD的外接圆交BC于点E,AC=CE=3,AB=4,则AD 的长为( )
如图,在△ABC中,CD是∠ACB的平分线,△ACD的外接圆交BC于点E,AC=CE=3,AB=4,则AD 的长为( )| A. | $\frac{3}{2}$ | B. | 2 | C. | $\frac{5}{2}$ | D. | 3 |
| A. | 在(0,+∞)上单调递增的奇函数 | B. | 在(0,+∞)上单调递减的奇函数 | ||
| C. | 在(0,+∞)上单调递增的偶函数 | D. | 在(0,+∞)上单调递减的偶函数 |