题目内容
3．设f（x）=$\left\{\begin{array}{l}{{e}^{\frac{1}{x}，x＜0}}\\{x+a，x≥0}\end{array}\right.$，问常数a为何值时，$\underset{lim}{x→0}$f（x）存在．分析 分别求得函数在零点的左右极限，当$\underset{lim}{x→{0}^{-}}$f（x）=$\underset{lim}{x→{0}^{+}}$f（x），即可求得a的值．
解答 解：函数在零点的左极限，$\underset{lim}{x→{0}^{-}}$f（x）=$\underset{lim}{x→{0}^{-}}$${e}^{\frac{1}{x}}$=0，
函数在零点的右极限，$\underset{lim}{x→{0}^{+}}$f（x）=$\underset{lim}{x→{0}^{+}}$（x+a）=a，
若极限存在，
则$\underset{lim}{x→{0}^{-}}$f（x）=$\underset{lim}{x→{0}^{+}}$f（x），
故a=0，
∴当a=0时，$\underset{lim}{x→0}$f（x）存在．
点评 本题考查极限存在条件，考查极限的运算，属于基础题．
练习册系列答案
相关题目
13．某电脑公司有6名产品推销员，其工作年限与年推销金额数据如表：
（1）求年推销金额y与工作年限x之间的相关系数（精确到0.01）；
（2）求年推销金额y关于工作年限x的线性回归方程．
（参考数据：$\sqrt{1.04}$≈1.02．）
参考公式：线性相关系数公式：r=$\frac{\sum_{i=1}^{n}（{x}_{i}-\overline{x}）（{y}_{i}-\overline{y}）}{\sqrt{\sum_{i=1}^{n}（{x}_{i}-\overline{x}）^{2}\sum_{i=1}^{n}（{y}_{i}-\overline{y}）^{2}}}$
线性回归方程系数公式：$\hat y$=bx+a，其中b=$\frac{\sum_{i=1}^{n}（{x}_{i}-\overline{x}）（{y}_{i}-\overline{y}）}{\sum_{i=1}^{n}（{x}_{i}-\overline{x}）^{2}}$，a=$\overline{y}$-bx．
| 推销员编号 | 1 | 2 | 3 | 4 | 5 |
| 工作年限x/年 | 3 | 5 | 6 | 7 | 9 |
| 推销金额y/万元 | 2 | 3 | 3 | 4 | 5 |
（2）求年推销金额y关于工作年限x的线性回归方程．
（参考数据：$\sqrt{1.04}$≈1.02．）
参考公式：线性相关系数公式：r=$\frac{\sum_{i=1}^{n}（{x}_{i}-\overline{x}）（{y}_{i}-\overline{y}）}{\sqrt{\sum_{i=1}^{n}（{x}_{i}-\overline{x}）^{2}\sum_{i=1}^{n}（{y}_{i}-\overline{y}）^{2}}}$
线性回归方程系数公式：$\hat y$=bx+a，其中b=$\frac{\sum_{i=1}^{n}（{x}_{i}-\overline{x}）（{y}_{i}-\overline{y}）}{\sum_{i=1}^{n}（{x}_{i}-\overline{x}）^{2}}$，a=$\overline{y}$-bx．
14．已知函数f（x）=2a-x2（$\frac{1}{e}$≤x≤e，e为自然数对数的底数）与g（x）=2lnx的图象上存在关于x轴对称的点，则实数a的最小值为（ ）
| A． | $\frac{1}{2}$ | B． | $\frac{1}{2e^2}$-1 | C． | $\frac{1}{2e^2}$+1 | D． | $\frac{e^2}{2}$-1 |
11．
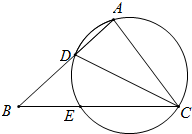如图，在△ABC中，CD是∠ACB的平分线，△ACD的外接圆交BC于点E，AC=CE=3，AB=4，则AD 的长为（ ）
如图，在△ABC中，CD是∠ACB的平分线，△ACD的外接圆交BC于点E，AC=CE=3，AB=4，则AD 的长为（ ）| A． | $\frac{3}{2}$ | B． | 2 | C． | $\frac{5}{2}$ | D． | 3 |
