题目内容
1.已知圆C:x2+y2-2x-6y+9=0,过x轴上的点P(1,0)向圆C引切线,则切线长为( )| A. | 3 | B. | 2$\sqrt{2}$ | C. | 2$\sqrt{3}$ | D. | 3$\sqrt{2}$ |
分析 根据圆的方程求出圆心和半径,求出PC的值,根据切线的长为$\sqrt{P{C}^{2}-{R}^{2}}$,运算求得结果.
解答 解:圆x2+y2-2x-6y+9=0 即 (x-1)2+(x-3)2=1,
表示以C(1,3)为圆心,半径R=1的圆.
PC=$\sqrt{(1-1)^{2}+(3-0)^{2}}$=3,故切线的长为$\sqrt{{3}^{2}-{1}^{2}}$=$2\sqrt{2}$,
故选:B.
点评 本题主要考查圆的标准方程,求圆的切线长的方法,属于中档题.

练习册系列答案
相关题目
9.命题“若m>0,则方程x2+x-m=0有实根”与其逆命题分别是( )
| A. | 真命题,真命题 | B. | 真命题,假命题 | C. | 假命题,真命题 | D. | 假命题,假命题 |
16.若不等式|x-2|+|x+3|<a的解集为∅,则a的取值范围为( )
| A. | (2,+∞) | B. | [-3,+∞) | C. | (-∞,5] | D. | (-∞,-3) |
13.某电脑公司有6名产品推销员,其工作年限与年推销金额数据如表:
(1)求年推销金额y与工作年限x之间的相关系数(精确到0.01);
(2)求年推销金额y关于工作年限x的线性回归方程.
(参考数据:$\sqrt{1.04}$≈1.02.)
参考公式:线性相关系数公式:r=$\frac{\sum_{i=1}^{n}({x}_{i}-\overline{x})({y}_{i}-\overline{y})}{\sqrt{\sum_{i=1}^{n}({x}_{i}-\overline{x})^{2}\sum_{i=1}^{n}({y}_{i}-\overline{y})^{2}}}$
线性回归方程系数公式:$\hat y$=bx+a,其中b=$\frac{\sum_{i=1}^{n}({x}_{i}-\overline{x})({y}_{i}-\overline{y})}{\sum_{i=1}^{n}({x}_{i}-\overline{x})^{2}}$,a=$\overline{y}$-bx.
| 推销员编号 | 1 | 2 | 3 | 4 | 5 |
| 工作年限x/年 | 3 | 5 | 6 | 7 | 9 |
| 推销金额y/万元 | 2 | 3 | 3 | 4 | 5 |
(2)求年推销金额y关于工作年限x的线性回归方程.
(参考数据:$\sqrt{1.04}$≈1.02.)
参考公式:线性相关系数公式:r=$\frac{\sum_{i=1}^{n}({x}_{i}-\overline{x})({y}_{i}-\overline{y})}{\sqrt{\sum_{i=1}^{n}({x}_{i}-\overline{x})^{2}\sum_{i=1}^{n}({y}_{i}-\overline{y})^{2}}}$
线性回归方程系数公式:$\hat y$=bx+a,其中b=$\frac{\sum_{i=1}^{n}({x}_{i}-\overline{x})({y}_{i}-\overline{y})}{\sum_{i=1}^{n}({x}_{i}-\overline{x})^{2}}$,a=$\overline{y}$-bx.
11.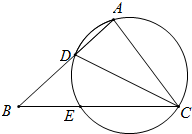 如图,在△ABC中,CD是∠ACB的平分线,△ACD的外接圆交BC于点E,AC=CE=3,AB=4,则AD 的长为( )
如图,在△ABC中,CD是∠ACB的平分线,△ACD的外接圆交BC于点E,AC=CE=3,AB=4,则AD 的长为( )
 如图,在△ABC中,CD是∠ACB的平分线,△ACD的外接圆交BC于点E,AC=CE=3,AB=4,则AD 的长为( )
如图,在△ABC中,CD是∠ACB的平分线,△ACD的外接圆交BC于点E,AC=CE=3,AB=4,则AD 的长为( )| A. | $\frac{3}{2}$ | B. | 2 | C. | $\frac{5}{2}$ | D. | 3 |
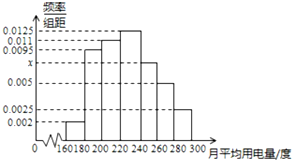 如图是某城市100户居民的月均用电量(单位:度)以[160,180),[180,200),[200,220),[220,240),[240,260),[260,280),[280,300]分组的频率分布直方图.
如图是某城市100户居民的月均用电量(单位:度)以[160,180),[180,200),[200,220),[220,240),[240,260),[260,280),[280,300]分组的频率分布直方图.