题目内容
6.甲手中有扑克牌的大小王牌和四色A各一张,共6张牌,现让乙和丙各从中随机抽取一张,则在乙抽到大王牌的情况下,丙抽到小王牌的概率为( )| A. | $\frac{1}{6}$ | B. | $\frac{1}{5}$ | C. | $\frac{1}{15}$ | D. | $\frac{1}{30}$ |
分析 设乙抽到大王,丙抽到小王,求出P(A),P(AB),由此利用条件概率计算公式能求出在乙抽到大王牌的情况下,丙抽到小王牌的概率.
解答 解:设乙抽到大王,丙抽到小王,
则P(A)=$\frac{1}{6}$,P(AB)=$\frac{1}{6}×\frac{1}{5}$=$\frac{1}{30}$,
∴在乙抽到大王牌的情况下,丙抽到小王牌的概率:
P(B|A)=$\frac{P(AB)}{P(A)}$=$\frac{\frac{1}{30}}{\frac{1}{6}}$=$\frac{1}{5}$.
故选:B.
点评 本题考查概率的求法,是中档题,解题时要认真审题,注意条件概率计算公式的合理运用.

练习册系列答案
相关题目
16.若不等式|x-2|+|x+3|<a的解集为∅,则a的取值范围为( )
| A. | (2,+∞) | B. | [-3,+∞) | C. | (-∞,5] | D. | (-∞,-3) |
14.已知函数f(x)=2a-x2($\frac{1}{e}$≤x≤e,e为自然数对数的底数)与g(x)=2lnx的图象上存在关于x轴对称的点,则实数a的最小值为( )
| A. | $\frac{1}{2}$ | B. | $\frac{1}{2e^2}$-1 | C. | $\frac{1}{2e^2}$+1 | D. | $\frac{e^2}{2}$-1 |
11.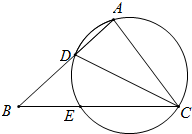 如图,在△ABC中,CD是∠ACB的平分线,△ACD的外接圆交BC于点E,AC=CE=3,AB=4,则AD 的长为( )
如图,在△ABC中,CD是∠ACB的平分线,△ACD的外接圆交BC于点E,AC=CE=3,AB=4,则AD 的长为( )
 如图,在△ABC中,CD是∠ACB的平分线,△ACD的外接圆交BC于点E,AC=CE=3,AB=4,则AD 的长为( )
如图,在△ABC中,CD是∠ACB的平分线,△ACD的外接圆交BC于点E,AC=CE=3,AB=4,则AD 的长为( )| A. | $\frac{3}{2}$ | B. | 2 | C. | $\frac{5}{2}$ | D. | 3 |
12.条件p:a≤3,条件q:a(a-3)≤0,则p是q的( )
| A. | 必要不充分条件 | B. | 充分不必要条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |