题目内容
2．
执行如图所示的程序框图，若输入的n的值为3，则输出的S的值为（ ）| A． | 2 | B． | 7 | C． | 17 | D． | 36 |
分析 模拟程序的运行过程，即可得出程序运行后输出的S值．
解答 解：模拟程序框图的运行过程，如下：
输入n=3，
k=1，S=0，进入循环，
S=0+1+21-1=2，k=2，k≤n；
S=2+2+22-1=7，k=3，k≤n；
S=7+3+23-1=17，k=4，k＞4；
终止循环，输出的S=17．
故选：C．
点评 本题主要考查了程序框图的应用问题，在写程序的运行结果时，常使用模拟循环的方法，是基础题．
练习册系列答案
快乐小博士巩固与提高系列答案
相关题目
13．某电脑公司有6名产品推销员，其工作年限与年推销金额数据如表：
（1）求年推销金额y与工作年限x之间的相关系数（精确到0.01）；
（2）求年推销金额y关于工作年限x的线性回归方程．
（参考数据：$\sqrt{1.04}$≈1.02．）
参考公式：线性相关系数公式：r=$\frac{\sum_{i=1}^{n}（{x}_{i}-\overline{x}）（{y}_{i}-\overline{y}）}{\sqrt{\sum_{i=1}^{n}（{x}_{i}-\overline{x}）^{2}\sum_{i=1}^{n}（{y}_{i}-\overline{y}）^{2}}}$
线性回归方程系数公式：$\hat y$=bx+a，其中b=$\frac{\sum_{i=1}^{n}（{x}_{i}-\overline{x}）（{y}_{i}-\overline{y}）}{\sum_{i=1}^{n}（{x}_{i}-\overline{x}）^{2}}$，a=$\overline{y}$-bx．
| 推销员编号 | 1 | 2 | 3 | 4 | 5 |
| 工作年限x/年 | 3 | 5 | 6 | 7 | 9 |
| 推销金额y/万元 | 2 | 3 | 3 | 4 | 5 |
（2）求年推销金额y关于工作年限x的线性回归方程．
（参考数据：$\sqrt{1.04}$≈1.02．）
参考公式：线性相关系数公式：r=$\frac{\sum_{i=1}^{n}（{x}_{i}-\overline{x}）（{y}_{i}-\overline{y}）}{\sqrt{\sum_{i=1}^{n}（{x}_{i}-\overline{x}）^{2}\sum_{i=1}^{n}（{y}_{i}-\overline{y}）^{2}}}$
线性回归方程系数公式：$\hat y$=bx+a，其中b=$\frac{\sum_{i=1}^{n}（{x}_{i}-\overline{x}）（{y}_{i}-\overline{y}）}{\sum_{i=1}^{n}（{x}_{i}-\overline{x}）^{2}}$，a=$\overline{y}$-bx．
7．在某校开展的“阳光体育”系列活动中，甲、乙两班之间进行了一次200米跑的团体比赛．每个班各派出5名同学比赛，讲每名同学的200米成绩记录以后（单位：秒，且已知每个成绩都是整数），总用时少的班级获胜，
成绩记录如表所示：
表格中的x∈[30，40）
（1）若x=36，从甲班的5名同学中任取3名，记这3人中用时少于乙队平均用时的人数为随机变量η，求η的分布列；
（2）若最终乙班获胜，那么当乙班同学的成绩方差最大时，x的取值是多少（直接写出结果，不用证明）？
成绩记录如表所示：
| 队员编号 | 1 | 2 | 3 | 4 | 5 |
| 甲班成绩 | 31 | 34 | 33 | 29 | 28 |
| 乙班成绩 | 27 | 31 | 30 | X | 31 |
（1）若x=36，从甲班的5名同学中任取3名，记这3人中用时少于乙队平均用时的人数为随机变量η，求η的分布列；
（2）若最终乙班获胜，那么当乙班同学的成绩方差最大时，x的取值是多少（直接写出结果，不用证明）？
14．已知函数f（x）=2a-x2（$\frac{1}{e}$≤x≤e，e为自然数对数的底数）与g（x）=2lnx的图象上存在关于x轴对称的点，则实数a的最小值为（ ）
| A． | $\frac{1}{2}$ | B． | $\frac{1}{2e^2}$-1 | C． | $\frac{1}{2e^2}$+1 | D． | $\frac{e^2}{2}$-1 |
11．
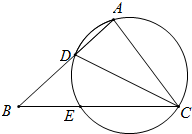如图，在△ABC中，CD是∠ACB的平分线，△ACD的外接圆交BC于点E，AC=CE=3，AB=4，则AD 的长为（ ）
如图，在△ABC中，CD是∠ACB的平分线，△ACD的外接圆交BC于点E，AC=CE=3，AB=4，则AD 的长为（ ）| A． | $\frac{3}{2}$ | B． | 2 | C． | $\frac{5}{2}$ | D． | 3 |