题目内容
3．若实数x，y满足xy=1，则x2+3y2的最小值为2$\sqrt{3}$．分析 利用基本不等式的性质即可得出．
解答 解：∵实数x，y满足xy=1，则x2+3y2的≥2$\sqrt{3}$xy=2$\sqrt{3}$，当且仅当$x=\sqrt{3}y$=±$\root{4}{3}$时取等号．
因此最小值为2$\sqrt{3}$．
故答案为：2$\sqrt{3}$．
点评 本题考查了基本不等式的性质，考查了推理能力与计算能力，属于基础题．
练习册系列答案
相关题目
13．两个整数1908和4187的最大公约数是（ ）
| A． | 53 | B． | 43 | C． | 51 | D． | 67 |
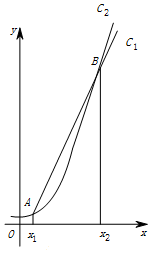函数f（x）=2x和g（x）=x3的图象的示意图如图所示，设两函数的图象交于点A（x1，y1），B（x2，y2），且x1＜x2．若x1∈[a，a+1]，x2∈[b，b+1]，且a，b∈{1，2，3，4，5，6，7，8，9，10，11，12}，则a+b=10．
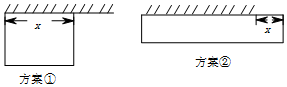上海市复兴高级中学二期改扩建工程于2015年9月正式开始，现需要围建一个面积火900平方米的矩形地场地的围墙，有一面长度为20米的旧墙（图中斜杠部），有甲、乙两种维修利用旧墙方案．
18．已知函数f（x）=ax2+2ax+4（-3＜a＜0），其图象上两点的横坐标为x1、x&2满足x1＜x2，且x1+x2=1+a，则由（ ）
| A． | f（x1）＜f（x2） | B． | f（x1）=f（x2） | ||
| C． | f（x1）＞f（x2） | D． | f（x1）、f（x&2）的大小不确定 |
15．判断函数f（x）=$\frac{{\sqrt{{x^2}+1}+x-1}}{{\sqrt{{x^2}+1}+x+1}}$的奇偶性（ ）
| A． | 奇函数 | B． | 偶函数 | ||
| C． | 既是奇函数又是偶函数 | D． | 非奇非偶函数 |