题目内容
已知函数f(x)=
x3-ax2+1.
(Ⅰ)若函数f(x)的图象关于点(0,1)对称,直接写出a的值;
(Ⅱ)求函数f(x)的单调递减区间;
(Ⅲ)若f(x)≥1在区间[3,+∞)上恒成立,求a的最大值.
| 1 |
| 3 |
(Ⅰ)若函数f(x)的图象关于点(0,1)对称,直接写出a的值;
(Ⅱ)求函数f(x)的单调递减区间;
(Ⅲ)若f(x)≥1在区间[3,+∞)上恒成立,求a的最大值.
考点:利用导数求闭区间上函数的最值,利用导数研究函数的单调性
专题:导数的综合应用
分析:(Ⅰ)利用y=
x3的对称中心,通过平移变换,函数f(x)的图象关于点(0,1)对称,直接写出a的值;
(Ⅱ)求出函数的导数,利用a与0大小比较,分类讨论通过等号的符号,求函数f(x)的单调递减区间;
(Ⅲ)利用f(x)≥1在区间[3,+∞)上恒成立,转化为a的不等式,然后求解最值,即可求a的最大值.
| 1 |
| 3 |
(Ⅱ)求出函数的导数,利用a与0大小比较,分类讨论通过等号的符号,求函数f(x)的单调递减区间;
(Ⅲ)利用f(x)≥1在区间[3,+∞)上恒成立,转化为a的不等式,然后求解最值,即可求a的最大值.
解答:
(共14分)
解:(Ⅰ)函数y=
x3的对称中心(0,0),平移变换后函数f(x)=
x3+1的对称中心(0,1),
∴a的值是0.…(2分)
(Ⅱ)f'(x)=x2-2ax.…(4分)
当a=0时,f'(x)≥0,f(x)在(-∞,+∞)内单调递增;
当a>0时,由f'(x)<0得:0<x<2a;
当a<0时,由f'(x)<0得:2a<x<0.…(7分)
综上所述,当a=0时,无递减区间;当a>0时,f(x)的单调递减区间是(0,2a);
当a<0时,f(x)的单调递减区间是(2a,0).
(Ⅲ)因为 f(x)≥1在区间[3,+∞)上恒成立,即
x3-ax2≥0在区间[3,+∞)上恒成立.
所以 a≤
x在区间[3,+∞)上恒成立.…(10分)
因为 x≥3,
所以
x≥1.…(11分)
所以 a≤1.…(13分)
所以 若f(x)≥1在区间[3,+∞)上恒成立,a的最大值为1.…(14分)
解:(Ⅰ)函数y=
| 1 |
| 3 |
| 1 |
| 3 |
∴a的值是0.…(2分)
(Ⅱ)f'(x)=x2-2ax.…(4分)
当a=0时,f'(x)≥0,f(x)在(-∞,+∞)内单调递增;
当a>0时,由f'(x)<0得:0<x<2a;
当a<0时,由f'(x)<0得:2a<x<0.…(7分)
综上所述,当a=0时,无递减区间;当a>0时,f(x)的单调递减区间是(0,2a);
当a<0时,f(x)的单调递减区间是(2a,0).
(Ⅲ)因为 f(x)≥1在区间[3,+∞)上恒成立,即
| 1 |
| 3 |
所以 a≤
| 1 |
| 3 |
因为 x≥3,
所以
| 1 |
| 3 |
所以 a≤1.…(13分)
所以 若f(x)≥1在区间[3,+∞)上恒成立,a的最大值为1.…(14分)
点评:本题考查函数的对称性,导函数求解函数的单调区间,函数的恒成立问题的应用,考查分类讨论转化思想的应用,是中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
下列四组函数中f(x)与g(x)是同一函数的是( )
A、f(x)=x,g(x)=
| |||||
B、f(x)=(
| |||||
| C、f(x)=2lgx,g(x)=lgx2 | |||||
D、f(x)=|x|,g(x)=
|
命题:“能被4整除的数一定是偶数”,其等价命题( )
| A、偶数一定能被4整除 |
| B、不是偶数不一定能被4整除 |
| C、不能被4整除的数不一定是偶数 |
| D、不是偶数一定不能被4整除 |
已知{an}是等差数列,其前n项和为Sn,若a3=7-a2,则S4=( )
| A、15 | B、14 | C、13 | D、12 |
已知集合A={0,1},B={x∈R|0<x<2},则A∩B=( )
| A、{0} | B、{1} |
| C、[0,1] | D、(0,1) |
已知函数f(x)=2mx3-3nx2+10(m>0)有且仅有两个不同的零点,则lg2m+lg2n的最小值为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
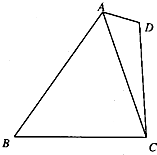 如图所示,在四边形ABCD中,∠D=2∠B,且AD=1,CD=3,cosB=
如图所示,在四边形ABCD中,∠D=2∠B,且AD=1,CD=3,cosB=