题目内容
在空间直角坐标系中有长方体ABCD-A′B′C′D′,且AB=2,AD=4,AA′=2,求平面AC′D与平面ABD夹角的余弦值.
考点:二面角的平面角及求法
专题:空间角
分析:首先做出面面夹角的平面角,进一步利用已知条件求出结果.
解答:
解:在空间直角坐标系中有长方体ABCD-A′B′C′D′,且AB=2,AD=4,AA′=2,
由于平面AC′D与面AC′D与平面ABD夹角的是同一个平面,
则:面AC′D与平面ABD夹角即面AC′D与平面ABD夹角的夹角.
由于:在长方体中,AB⊥AD,AB′⊥AD,
所以:∠BAB′即为平面AC′D与平面ABD所成交的平面角.
cos∠BAB′=
=
由于平面AC′D与面AC′D与平面ABD夹角的是同一个平面,
则:面AC′D与平面ABD夹角即面AC′D与平面ABD夹角的夹角.
由于:在长方体中,AB⊥AD,AB′⊥AD,
所以:∠BAB′即为平面AC′D与平面ABD所成交的平面角.
cos∠BAB′=
| BB′ |
| AB′ |
| ||
| 2 |
点评:本题考查的知识要点:二面角的应用,属于基础题型.

练习册系列答案
 春雨教育同步作文系列答案
春雨教育同步作文系列答案
相关题目
已知a≥1,f(x)=x3+3|x-a|,若函数f(x)在[-1,1]上的最大值和最小值分别记为M、m,则M-m的值为 C( )
| A、8 |
| B、-a3-3a+4 |
| C、4 |
| D、-a3+3a+2 |
非空数集A={a1,a2,a3,…,an}(n∈N*)中,所有元素的算术平均数记为E(A),即E(A)=
.若非空数集B满足下列两个条件:①B⊆A;②E(B)=E(A).则称B是A的一个“保均值子集”.据此,集合{2,3,4,5,6}的“保均值子集”有( )
| a1+a2+a3+…+an |
| n |
| A、5个 | B、6个 | C、7个 | D、8个 |
若f(x)=x2+(4cosθ)x-1在[1,
]上为增函数,则θ的取值范围是( )
| 3 |
A、[2kπ-
| ||||
B、[2kπ-
| ||||
C、[2kπ+
| ||||
D、[2kπ-
|
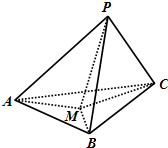 如图,在三棱锥P-ABC中,PA、PB、PC两两互相垂直,且PA=3,PB=2,PC=1,设M是底面ABC内一点,定义f(M)=(m,n,p),其中m,n,p分别是三棱锥M-PAB、三棱锥M-PBC、三棱锥M-PCA的体积,若f(M)=(
如图,在三棱锥P-ABC中,PA、PB、PC两两互相垂直,且PA=3,PB=2,PC=1,设M是底面ABC内一点,定义f(M)=(m,n,p),其中m,n,p分别是三棱锥M-PAB、三棱锥M-PBC、三棱锥M-PCA的体积,若f(M)=(