题目内容
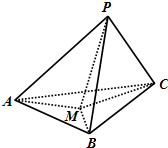 如图,在三棱锥P-ABC中,PA、PB、PC两两互相垂直,且PA=3,PB=2,PC=1,设M是底面ABC内一点,定义f(M)=(m,n,p),其中m,n,p分别是三棱锥M-PAB、三棱锥M-PBC、三棱锥M-PCA的体积,若f(M)=(
如图,在三棱锥P-ABC中,PA、PB、PC两两互相垂直,且PA=3,PB=2,PC=1,设M是底面ABC内一点,定义f(M)=(m,n,p),其中m,n,p分别是三棱锥M-PAB、三棱锥M-PBC、三棱锥M-PCA的体积,若f(M)=(| 1 |
| 2 |
| 1 |
| x |
| a |
| y |
考点:棱柱、棱锥、棱台的体积,基本不等式
专题:空间位置关系与距离
分析:由题设和(M)的意义可得x+y=
,由此能求出正实数a的最小值.
| 1 |
| 2 |
解答:
解:由题设知VP-ABC=VA-BPC=
S△PBC•PA=1,
于是依f(M)的意义可得
+x+y=1,即有x+y=
,
从而
+
=(
+
)•2(x+y)=2[1+a+(
+
)]≥2(1+a+2
)=2(1+
)2,
(其中等号当且仅当
=
即y=
x时成立.)
∴由
+
≥8恒成立,得2(1+
)2≥8,
解得a≥1.
∴正实数a的最小值为1.
故答案为:1.
| 1 |
| 3 |
于是依f(M)的意义可得
| 1 |
| 2 |
| 1 |
| 2 |
从而
| 1 |
| x |
| a |
| y |
| 1 |
| x |
| a |
| y |
| y |
| x |
| ax |
| y |
| a |
| a |
(其中等号当且仅当
| y |
| x |
| ax |
| y |
| a |
∴由
| 1 |
| x |
| a |
| y |
| a |
解得a≥1.
∴正实数a的最小值为1.
故答案为:1.
点评:本题考查满足条件的实数的最小值的求法,解题时要注意棱锥的体积、均值定理的合理运用,是中档题.

练习册系列答案
相关题目
一个袋中装有3个红球和3个白球,现从袋中取出1球,然后放回袋中再取出一球,则取出的两个球是同色球的概率是( )
A、
| ||
B、
| ||
C、
| ||
D、
|
已知对任意的x,y∈R,都有f(x)+f(y)=2f(
)•f(
),f(0)≠0,则f(x)为( )
| x+y |
| 2 |
| x-y |
| 2 |
| A、是奇函数 |
| B、是偶函数 |
| C、既是奇函数又是偶函数 |
| D、无法确定f(x)奇偶性 |
已知圆O1:x2+y2=1与圆O2:x2+y2-6x+8y+9=0,则两圆的位置关系为( )
| A、相交 | B、内切 | C、外切 | D、相离 |
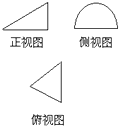 如图是某几何体的三视图,其中正视图是斜边长为2a的直角三角形,侧视图是半径为a的半圆,则该几何体的体积是( )
如图是某几何体的三视图,其中正视图是斜边长为2a的直角三角形,侧视图是半径为a的半圆,则该几何体的体积是( )A、
| ||||
B、
| ||||
C、
| ||||
D、2
|
不等式x2-2x-3<0的解集是( )
| A、{x|x<-1} |
| B、{x|x>3} |
| C、{x|-1<x<3} |
| D、{x|x<-1或x>3} |
 如图,已知长方体ABCD-A1B1C1D1中,AB=2
如图,已知长方体ABCD-A1B1C1D1中,AB=2